پیاده سازی تابع لگاریتم در FPGA

مقدمه

یکی از مهترین ویژگی‌های تراشه‌های FPGA قابلیت‌های آن‌ها در پیاده‌سازی انواع توابع ریاضی است. توابع ریاضی ممکن است گاهاً بسیار ساده و ترکیبی از چند عمل ضرب و جمع باشند. بعضاً نیز ممکن است شامل عملگرهای غیرخطی همچون لگاریتم یا توابع مثلثاتی باشند. اگر مدت‌هاست با تراشه های FPGA کار می‌کنید، مطمئناً می‌دانید که برای پیاده‌سازی تابع لگاریتم IP Core آماده وجود ندارد. پس در صورتی که نیار به پیاده سازی تابع لگاریتم در یک الگوریتم داشته باشید باید خودتان آستین‌ها را بالا بزنید و کار را شروع کنید.

اولین راه حلی که ممکن است به ذهن طراح برسد، استفاده از یک حافظه ROM است. در این روش مقدار تابع لگاریتم (x‏)log به ازای مقادیر مختلف ورودی x در نرم افزار Matlab محاسبه می‌شود و سپس این مقادیر درون حافظه‌های FPGA ذخیره می‌شوند. در عمل به ازای مقادیر مختلف x یک آدرس از حافظه انتخاب می‌شود، و محتوای ذخیره شده در آن آدرس مقدار تابع (x‏)log است. اما این روش چند عیب دارد:

• در این روش نیاز به یک مدار اضافی برای کنترل و نگاشت مقادیر x به آدرس‌های حافظه داریم.
• در صورت نیاز به دقت بالا برای خروجی تابع لگاریتم عرض بیت مقادیری که در حافظه ذخیره می‌شوند، افزایش می‌یابد و منجربه بزرگ شدن سایز حافظه می‌شود.
• در صورتی که بازه تغییرات ورودی x زیاد باشد، به ناچار باید برای پوشش کل بازه از حافظه‌های بزرگ استفاده کنیم، که معمولا با ترکیب چند بلوک حافظه ساخته می‌شوند.

با وجود این در بسیاری از موارد ممکن است استفاده از حافظه ROM بهترین و ساده‌ترین گزینه باشد. اما سوأل اینجاست، اگر این کار امکان پذیر نبود چه باید کرد؟ لازم نیست نگران باشید. با چند تکنیک ساده این مسأله قابل حل است. با توجه به اینکه محاسبه لگاریتم در چه مبنایی مورد نیاز است، ممکن است میزان محاسبات مورد نیاز برای دستیابی به پاسخ مطلوب متفاوت باشد. در این آموزش ما کار را با محاسبه عبارت (x‏)log₂ شروع می‌کنیم. سپس بحث را گسترش می‌دهیم و محاسبه لگاریتم در سایر مبنا‌ها و یکسری از شرایط خاص را نیز پوشش می‌دهیم. برای درک بهتر مسأله توضیحات همراه با مثال ارائه شده است.

لگاریتم در مبنای ۲

در حالت کلی پیاده‌سازی عبارت (x‏)log₂ در FPGA به ازای هر مقدار x دارای یک بخش صحیح و یک بخش اعشاری است. به عنوان مثال برای عدد ۵۳ خواهیم داشت.

$$Log_2(53) = 5.72792045 = 5.7279$$

مقدار 5 نشان دهنده مقدار صحیح و مقدار 0.7279 بیانگر مقدار اعشاری است. به صورت پیش فرض برای محاسبه (x‏)log₂ یک در آن x یک عدد N بیتی است، ابتدا مقدار صحیح و سپس مقدار اعشاری پاسخ را محاسبه می‌کنیم.

محاسبه بخش صحیح که از این پس آن را با نماد S نمایش می دهیم، یک کار نسبتا آسان است. فقط کافی است موقعیت اولین بیت با ارزشی را که مقدار آن ‘1’ است، پیدا کنیم. در مثال عدد ۵۳ در یک نمایش ۸ بیتی به صورت زیر، موقعیت اولین بیت ‘1’ با ۵ است. برای پیدا کردن اولین ‘1’ می‌توان از تابعی تحت عنوان LeadOneDetector استفاده کرد.

در ادامه M بیت بعد از اولین ‘1’ را  انتخاب می‌کنیم. ما از این M بیت برای تعیین بخش اعشاری (x‏)log₂ استفاده می‌کنیم. چگونگی انتخاب مقدار مناسب برای M در ادامه توضیح داده می‌شود فعلاً از بیان جزئیات بیشتر در این بخش پرهیز می‌کنیم. برای تعیین بخش اعشاری که از این پس آن را با نماد F نمایش می‌دهیم، نیاز به یک حافظه داریم که در آن 2^M مقدار را ذخیره کنیم (چرا؟). این 2^M مقدار، مقادیر حاصل از محاسبه عبارت (y‏)log₂ است. که در آن مقدار y برابر است با:

$$y=1+m/2^M$$

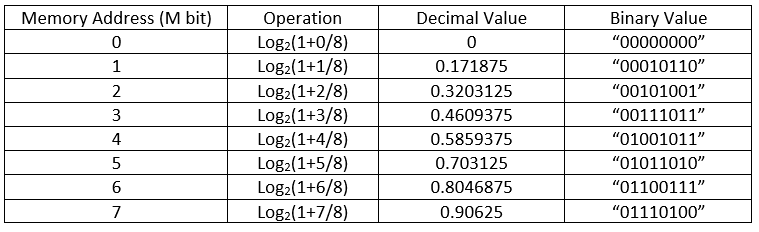
و در انتهای کار مقدار (53‏)log₂ به صورت حاصل جمع مقدار صحیح و مقدار اعشار به صورت زیر قابل محاسبه است. با تقریب نسبتا خوبی معادل نتایج Matlab است، اینطور نیست؟

$$Log_2 (53) = S + F = 5.7031$$

خب به نظر می‌رسد، کار خیلی سختی نداشتیم. مسأله‌ای را که در ابتدا پیچیده به نظر می‌رسید به سادگی حل کردیم. حالا فرض می‌کنیم که مقدار تقریبی بدست آمده برای ما مطلوب نیست و نیاز داریم، تخمین دقیق‌تری از عبارت لگاریتم بدست بیاوریم. به نظر شما آیا می‌توان دقت محاسبات را افزایش داد؟ پاسخ به این سوال بله است. در ازای پرداخت هزینه می‌توان تخمین دقیق‌تری از عبارت (x‏)log₂ ارائه داد است. به طور کلی برای افزایش دقت دو راه وجود دارد.

• مقادیر اعشاری محاسبه شده در Matlab را با رزولوشن بالاتری ذخیره کنیم و تعداد بیت بیشتری به آن اختصاص دهیم.
• تعداد مقادیر اعشاری بیشتری را ذخیره کنیم و گام‌های پرش روی مقادیر ذخیره شده در حافظه را کوچکتر کنیم، به بیان ساده تر M را بزرگتر انتخاب کنیم.

با افزایش مقدار M (بیت‌های مورد نیاز برای محاسبه بخش اعشاری) سایز حافظه به صورت نمایی زیاد می‌شود. پس بهتر است برای بزرگتر کردن مقدار M عجله نکنیم و یک مصالحه بین دقت و منابع مصرفی ایجاد کنیم.

براساس تجربه شش بیت برای بدست آوردن دقت قابل قبول کفایت می‌کند. این یعنی M=6 در نظر بگیریم. برای ذخیره سازی مقادیر محاسبه شده در Matlab نیز می‌توان از کلمه‌های ۱۶ بیتی استفاده کرد. در این صورت تنها با استفاده از شانزده LUT می‌توان طراحی حافظه را انجام داد. (چرا؟)

اگر فکر می‌کنید که کار تمام شده و تمام ملاحظات را در نظر گرفتیم، باید بگویم که متأسفانه اشتباه می‌کنید. هنوز یک نکته بسیار مهم باقیمانده است. جمع کردن مقادیر اعشاری و صحیح نیاز به کمی دقت دارد. در هنگام جمع باید بیت‌های با ارزش یکسان در جایگاه اصلی خودشان نوشته شوند و با هم جمع شوند. زیرا ۸ بیت حاصل از قسمت اعشاری با ۳ بیت حاصل از قسمت صحیح با هم، هم ارزش نیستند. برای روشن شدن موضوع به شکل زیر دقت کنید.

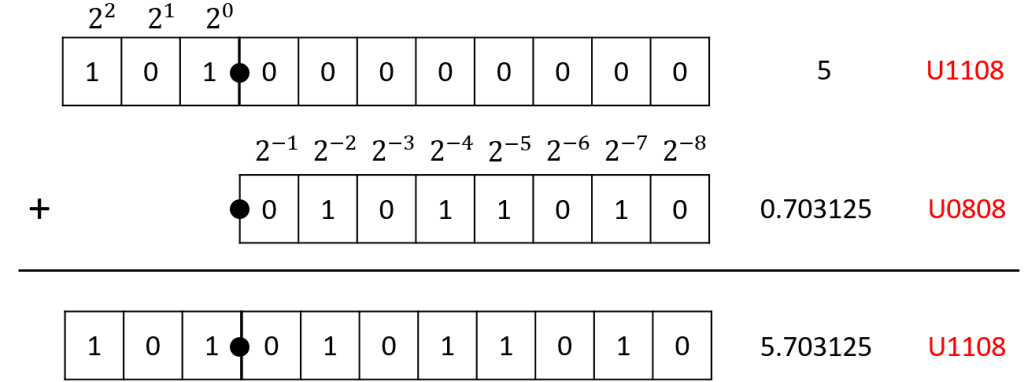
کلید طلایی پیاده سازی

اگر در پیاده‌سازی نهایی تعداد بیت‌های باقی مانده بعد از اولین ‘1’ کمتر از M بیتِ در نظر گرفته شده برای آدرس باشد، ممکن است عملکرد صحیح مدار مختل شود و در هنگام سنتز خطا داشته باشیم. (چرا؟) از این رو بهتر است در صورت رخ دادن چنین شرایطی یک شرط اضافی در طراحی در نظر بگیریم و به صورت ثابت آدرس حافظه را برابر با 2^M-1-1 در نظر بگیریم. این کار باعث سادگی پیاده‌سازی با یک دقت خوب می‌شود. در مثال عدد ۵۳ برای M=6 مقدار ۳۱ حاصل می شود. بهتر است این عدد به عنوان آدرس جایگزین بیت‌های انتخابی از ورودی x شود.

جمع کردن مقادیر اعشاری و صحیح نیاز به کمی دقت دارد، در هنگام جمع باید بیت‌های با ارزش یکسان در جایگاه اصلی خودشان نوشته شوند

لگاریتم طبیعی و لگاریتم در مبنای ۱۰

حالا که تقریبأ تمامی جزئیات مورد نیاز برای پیاده سازی بهینه تابع (x‏)log₂ را مرور کردیم، اجازه بدهید بحث را کمی گسترش بدهیم و راه حلی برای محاسبه توابعی همچون (x‏)ln و یا (x‏)log₁₀ ارائه بدهیم. به نظر شما برای برای محاسبه عبارت ‏(x‏)‏log₁₀‏ × ‏10 چه باید کرد؟ این رابطه به شکل گسترده‌ای در مخابرات مورد استفاده قرار می‌گیرد. آیا می‌توان از روشی که توضیحات آن ارائه شد استفاده کرد؟ پاسخ به این سوأل هم بله است. کلید حل مسأله در ریاضیات پایه و آشنایی با خواص لگاریتم است.

در رابطه زیر با استفاده از خواص تابع لگاریتم عبارت (x‏)log₁₀ را بر اساس عبارت (x‏)log₂ بازنویسی کردیم. سپس با کمک Matlab، حاصل ضرب مقادیر ثابت را محاسبه کردیم و به صورت یک ضریب برای عبارت (x‏)log₂ در نظر گرفتیم. یعنی هزینه نهایی پیاده‌سازی تنها یک عملیات ضرب بیشتر نسبت به حالت قبل است. برای (x‏)ln نیز می‌توان به روش مشابه عمل کرد.

$$f(x) =10\times log_2{10}(x)={10\times log_2(x)}/{log_2(10)}=3.01 \times log_2(x)$$

می‌توان با استفاده از خواص تابع لگاریتم عبارت (x‏)log₁₀ را بر اساس عبارت (x‏)log₂ بازنویسی کرد

فانکشن متلب نوشته شده برای محاسبه عبارت ‏(x‏)‏log₁₀‏ × ‏10 به صورت زیر است. این فانکشن هر مقدار x بین صفر تا ۶۵۵۳۵.۹۹۹ ابتدا در یک متغیر ۳۲ بیتی ذخیره می‌کند، سپس جستجو برای یافتن موقعیت اولین ‘1’ را آغاز می‌کند.

% copyright 2019 Hexalinx.com

function fixedpoint_10log10(x)
f = fimath('OverflowAction','Wrap','RoundingMethod','Floor');

Q3216 = numerictype(1,32,16);
Q1815 = numerictype(1,18,15);
Q1813 = numerictype(1,18,13);
Q1810 = numerictype(1,18,10);

x_fi = fi(x,Q3216,f);

Nx   = x_fi.WordLength;
Fx   = x_fi.FractionLength;

n    = 6;                               % LUT ROM resolution
L    = 2^n;                             % LUT ROM length
LUT  = fi(log2(1+(0:(L-1))/L),Q1813,f); % LUT ROM
m    = strfind(x_fi.bin,'1');           % LOD
a    = bin2dec(x_fi.bin(m+1:m+n));      % LUT ROM addr

S    = fi(Nx-Fx-m(1),Q1813,f);
F    = LUT(a+1);

temp = fi(3.0103,Q1815,f)*fi((S+F),Q1813,f);

hardware = fi(temp,Q1810,f);
golden   = 10*log10(x);

disp(['hardware = ' num2str(hardware.data)]);
disp(['golden   = ' num2str(golden)]);

محاسبه لگاریتم برای اعداد ممیز ثابت

آخرین و احتمالاً بحث پرچالش‌ترین بخشی که هنوز از مبحث محاسبه لگاریتم باقی مانده مربوط به محاسبات ممیز ثابت است. در عمل اعدادی که در محاسبات پردازش سیگنال مورد استفاده قرار می‌گیرند، اعداد صحیح نیستند. به نظر شما برای محاسبه لگاریتم عدد x که به صورت ممیز ثابت یا در اصطلاح fixed point تعریف شده است و تعدادی بیت اعشاری دارد، چگونه باید عمل کنیم؟

قبل از پاسخ به سوأل بالا بهتر است یادآوری کنم که لگاریتم فقط برای اعداد مثبت محاسبه می‌شود. ولی در حالتی که عدد x ممیز ثابت باشد بهتر است این عدد به صورت علامت دار با علامت مثبت ذخیره بشود؟ (چگونه؟) مثلا اگر عدد ۵۳ را با ۱۲ بیت صحیح و ۴ بیت اعشاری نشان دهیم، ارزش مقادیر آن‌ها به صورت شکل زیر خواهد بود.

در این شکل نقطه سیاه رنگ مکان فرضی نقطه اعشار را نشان می‌دهد. به طور کلی طراحان FPGA و به ویژه شرکت Xilinx توصیه می‌کنند که برای انجام محاسبات ریاضی اعداد به صورت علامت دار در محاسبات شرکت داده شوند. در این صورت محاسبات با دقت و ضریب اطمینان بالاتری انجام می‌شوند.

همانطور که اشاره شد برای پیدا کردن اولین ‘1’ می‌توان از تابعی تحت عنوان LeadOneDetector استفاده کرد. زمانی که در محاسبات با یک عدد ممیز ثابت روبرو هستیم، باید تغییرات کوچکی در این تابع اعمال کنیم و موقعیت اولین بیت را با توجه به تعداد بیت‌های صحیح بسنجیم. یعنی تعداد بیت‌های اعشاری ورودی x را از عدد خروجی تابع LeadOneDetector کم کنیم. درمثال عدد ۵۳ در صورت استفاده از نمایش ۱۶ بیتی فوق موقعیت اولین بیت توسط تابع LOD برابر با ۹ گزارش می‌شود. برای به دست آوردن موقعیت واقعی آن لازم است یک تفریق انجام شود، و عبارت 5=4-9 محاسبه شود.

ماژول HDL معادل با فانکشن fixedpoint_10log10 نیز به صورت زیر است. در این ماژول ورودی‌ها ۱۸ بیتی هستند و تعداد بیت اعشار آن‌ها نیز ۱۷ بیت در نظر گرفته شده است. بدیهی است که تفاوتی نمی‌کند ورودی‌ها چند بیتی باشند. برای نوشتن این کد از پکیج conv_pkg.vhd استفاده شده است که جز پکیج‌های استاندارد ابزار System Generator است. شما می‌توانید این فایل را از اینجا دانلود کنید.

-- copyright 2019 Hexalinx.com

library IEEE;
use IEEE.STD_LOGIC_1164.ALL;
use IEEE.NUMERIC_STD.ALL;

library work;
use work.conv_pkg.all;

entity fixedpoint_10log10 is
    generic ( INPUT_WORD_LEN  : natural := 18;
              INPUT_FRAC_LEN  : natural := 17;
              OUTPUT_WORD_LEN : natural := 18);
    Port    ( Clk             : in  STD_LOGIC;
              Rst             : in  STD_LOGIC;
              Valid_i         : in  STD_LOGIC;
              Data_i          : in  STD_LOGIC_VECTOR (INPUT_WORD_LEN-1 downto 0);
              Valid_o         : out  STD_LOGIC;
              Data_o          : out  STD_LOGIC_VECTOR (OUTPUT_WORD_LEN-1 downto 0)); -- Q1810
end fixedpoint_10log10;

architecture Behavioral of fixedpoint_10log10 is

    constant COEFF : signed := to_signed(98641,18); -- 0.30103=10*log10(2), Q1815
    constant NX    : natural := 32;
    constant FX    : natural := 16;
    constant n     : natural := 6;
   
    type FRACTION_LUT_TYPE is array (0 to 2**n-1) of std_logic_vector(18-1 downto 0);
    constant fractionLUT : FRACTION_LUT_TYPE := (
    "000000000000000000",   "000000000010110111",   "000000000101101011",   "000000001000011101",
    "000000001011001100",   "000000001101111001",   "000000010000100011",   "000000010011001010",
    "000000010101110000",   "000000011000010011",   "000000011010110011",   "000000011101010010",
    "000000011111101111",   "000000100010001001",   "000000100100100010",   "000000100110111000",
    "000000101001001101",   "000000101011100000",   "000000101101110001",   "000000110000000000",
    "000000110010001101",   "000000110100011001",   "000000110110100011",   "000000111000101100",
    "000000111010110011",   "000000111100111001",   "000000111110111101",   "000001000000111111",
    "000001000011000001",   "000001000101000000",   "000001000110111111",   "000001001000111100",
    "000001001010111000",   "000001001100110010",   "000001001110101011",   "000001010000100011",
    "000001010010011010",   "000001010100010000",   "000001010110000100",   "000001010111110111",
    "000001011001101010",   "000001011011011011",   "000001011101001011",   "000001011110111010",
    "000001100000101000",   "000001100010010100",   "000001100100000000",   "000001100101101011",
    "000001100111010101",   "000001101000111110",   "000001101010100111",   "000001101100001110",
    "000001101101110100",   "000001101111011010",   "000001110000111110",   "000001110010100010",
    "000001110100000101",   "000001110101100111",   "000001110111001000",   "000001111000101001",
    "000001111010001000",   "000001111011100111",   "000001111101000101",   "000001111110100011");

    signal X : std_logic_vector(NX-1 downto 0) := (others => '0');
    signal S : signed(18-1 downto 0) := (others => '0');          -- Q1813
    signal F : signed(18-1 downto 0) := (others => '0');          -- Q1813
    signal Y : signed(36-1 downto 0) := (others => '0');          -- Q3628
    signal m : integer range 0 to NX-1 := 0;
    signal a : integer range 0 to 2**n-1 := 0;
    signal t : std_logic_vector(6-1 downto 0) := (others => '0'); -- intermediate var. for S Calculation

    signal valid_r1,valid_r2 : std_logic := '0';                  -- input valid registers
   
    function LeadOneDetector(Input : std_logic_vector)   return integer is
        constant LEN : integer := Input'length;
        variable Idx : integer range 0 to LEN-1;
    begin
        Idx := 0;
        looop:
        for i in 0 to LEN-1 loop
            if Input(i) = '1' then 
                Idx := i;
            end if;
        end loop;
        return Idx;
    end function LeadOneDetector;
      
begin
   
    -- convert input to 32 bit signal with 16 fraction bit
    X <= convert_type(Data_i, INPUT_WORD_LEN, INPUT_FRAC_LEN, xlSigned, NX, FX, xlSigned, xltruncate, xlwrap);

    -- find the leading '1' position
    m_proc:
    process(Clk)
    begin
        if rising_edge(Clk) then
            -- latch the input signal
            if valid_i = '1' then 
                m <= LeadOneDetector(X);
            end if;
            -- pipeline shift register for contقol signal
            Valid_r1 <= Valid_i;
            Valid_r2 <= Valid_r1;
            Valid_o  <= Valid_r2;
        end if;
    end process;

    -- calculate the integer part (intermediate var.)
    t <= std_logic_vector(to_signed(m-FX,6));

    -- calculate the address for fraction part with some approximation for resource control
    a <= to_integer(unsigned(X(m-1 downto m-n))) when m >= n-1 else  31;

    -- register in pre-adder
    ad_proc:
    process(Clk)
    begin
        if rising_edge(Clk) then
            if Rst = '1' then
                S <= (others => '0');
                F <= (others => '0');
            else
                S <= signed(convert_type(t, 6, 0, xlSigned, 18, 13, xlSigned, xltruncate, xlwrap));
                F <= signed(fractionLUT(a)); -- read the fractional part from address <a>   
            end if;
        end if;
    end process;

    -- register in pre-adder
    p_proc:
    process(Clk)
    begin
        if rising_edge(Clk) then
            if Rst = '1' then
                Y <= (others => '0');
            else
                Y <= (S + F) * COEFF ; -- ( Q1813 + Q1813 ) * Q1815   
            end if;
        end if;
    end process;
   
    Data_o <= convert_type(std_logic_vector(Y), 36, 28, xlSigned, 18, 10, xlSigned, xltruncate, xlwrap);
   
end Behavioral;

آموزش ویدئویی

اگر همچنان در درک کامل روشی که توضیح داده شده مشکل دارید. پیشنهاد می‌کنم حتما ویدئوهای آموزشی زیر را مشاهده بفرمایید.

قسمت اول

قسمت دوم

جمع بندی

پیاده‌سازی بسیاری از الگوریتم‌های پردازش سیگنال به صورت مستقیم امکان پذیر نیست و طراح باید با استفاده از تجربه و دانش خود محاسبات را به بخش‌های کوچتر تقسیم کند و با شکستن الگوریتم یا تابع آن را قابل پیاده‌سازی کند. مثال خوبی از این شیوه پیاده‌سازی تابع لگاریتم است. در این مقاله یک روش ساده و بسیار کم هزینه به لحاظ منابع مصرفی برای پیاده‌سازی لگاریتم ارائه دادیم که می‌تواند بر حسب نیاز در سیستم‌های مخابراتی و یا الگوریتم‌های هوش مصنوعی بکارگرفته شود. امیدوارم آموزش پیاده‌سازی تابع لگاریتم در FPGA برای شما هم مفید بوده باشد.