مبانی محاسبات ریاضی در FPGA (قسمت اول)

مقدمه

یکی از مهمترین مزایای طراحی‌های مبتنی بر تراشه‌های قابل پیکره‌بندی توانایی آن‌ها در پیاده‌سازی الگوریتم‌های ریاضی به بهترین شکل ممکن است. برای مثال اگر برای دست‌یابی به پاسخ نهایی محدودیت زما‌نبندی وجود دارد، می‌توان از پایپلاین کردن در بین گام‌های اجرای محاسبات استفاده کرد. اما اگر دقت نهایی اهیمت بیشتری دارد، می‌توان از تعداد بیت‌های بیشتری برای دستیابی به دقت مطلوب استفاده کرد. البته تقریبا تمامی تراشه‌های قابل پیکره‌بندی مجهز به بلوک‌های ضرب کننده DSP هستند که کمک فراوانی به پیاده‌سازی بهینه الگوریتم‌های ریاضی می‌کند.

در این آموزش از پایگاه دانش هگزالینکس قصد داریم مروری بر مبانی محاسبات ریاضی در FPGA داشته باشیم. اجازه بدهید با هم نگاهی بیاندازیم به قوانین و تکنیک‌هایی که شما می‌توانید برای توسعه یک تابع ریاضی روی تراشه‌های قابل پیکره‌بندی بکار بگیرد.

نمایش اعداد

در حالت کلی دو الگوی کلی برای نمایش اعداد درون یک طراحی دیجیتال وجود دارد.

• سیستم نمایش اعداد ممیز ثابت و
• سیستم نمایش اعداد ممیز شناور.

سیستم نمایش ممیز ثابت، موقعیت نقطه اعشار را ثابت نگه می‌دارد، به این ترتیب می‌توان عملیات ریاضی را کاملا سرراست انجام داد. مهمترین نقطه ضعف سیستم ممیز ثابت این است که برای نشان دادن اعداد بزرگتر با هدف رسیدن به نتیجه دقیق‌تر باید از تعداد بیت بیشتری برای نمایش بخش اعشاری استفاده کرد. هر عدد ممیز ثابت از دو بخش صحیح و اعشاری تشکیل شده است.

در سیستم نمایش ممیز شناور، نقطه اعشار با توجه به اندازه عدد، می‌تواند به مکان‌های مختلف در داخل عدد منتقل یا در اصطلاح شناور شود. اعداد ممیز شناور نیز به دو بخش مانتیس و توان تقسیم می‌شوند. این سیستم نمایش بسیار شبیه به شیوه نمایش علائم علمی است، که در آن عدد A را به صورت ضریبی برای عدد پایه ۱۰ به توان B  نشان داده‌ می‌شود، یعنی Ax10^B. در اینجا A معرف مانتیس و B نماینده توان یا نما است. با این تفاوت که، پایه مورد استفاده برای نمایش در یک عدد ممیز شناور برابر با ۲ است، یعنی A ضربدر ۲ به توان B. اعداد ممیز شناور توسط  IEEE/ANSI standard 754-1985 استاندارد شده‌اند. در نمایش استاندارد یک عدد ممیز ثابت ۸ بیت به نمایش توان و ۲۴ بیت برای نمایش مانتیس اختصاص داده شده است.

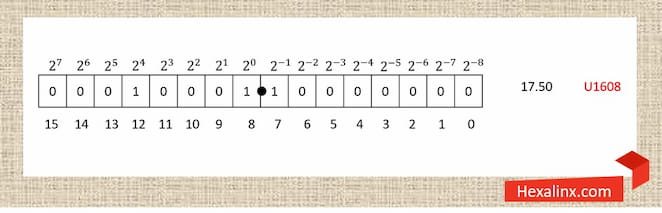
به دلیل پیچیدگی سیستم اعداد ممیز شناور، ما به عنوان طراح هر جا ممکن باشد از نمایش‌های ممیز ثابت استفاده می‌کنیم. عدد ۱۶ بیتی ممیز ثابت زیر قادر به نمایش اعداد بدون علامت در بازه 0.0 تا 255.9906375 است. در صورت علامت دار بودن قادر به نمایش اعداد بین 128.9906375- تا 127.9906375 بر اساس روش نمایش مکمل دو است. درون طرح شما به عنوان طراح با توجه به الگوریتمی که در حال پیاده‌سازی آن هستید، انتخاب می‌کنید که از اعداد علامت دار یا بدون علامت استفاده کنید.

دامنه تغییرات اعداد علامت دار و بدون علامت با هم متفاوت است. برای اعداد بدون علامت دامنه تغییرات محدود به بازه صفر تا 2^N-1 است. اما در مقابل، دامنه تفییرات یک عدد علامت دار با توجه به روش نمایش آن متغیر است. اعداد علامت دار با توجه به یکی از روش‌های علامت اندازه، مکمل یک و مکمل دو نمایش داده می‌شوند.

در روش نمایش علامت و اندازه از بیت چپ برای نشان دادن علامت عدد (0 = مثبت ، 1 = منفی) استفاده می‌شود. بیت‌های باقیمانده اندازه را نشان می‌دهند. بنابراین، در این شیوه نمایش، اعداد مثبت و منفی دارای اندازه یکسان هستند اما بیت علامتشان متفاوت است. در نتیجه، این روش نمایش دارای دو مقدار صفر است یعنی درای یک صفر مثبت و منفی است.

نمایش اعداد مثبت در روش مکمل یک مشابه روش علامت اندازه است، اما برای اعداد منفی از وارونگی (مکمل یک) عدد مثبت استفاده می‌شود.

روش مکمل دو پر استفاده‌ترین شیوه نمایش اعداد علامت دار است. در اینجا هم، مانند دو روش دیگر، اعداد مثبت به همان ترتیب اعداد بدون علامت نمایش داده می‌شوند. در حالی که اعداد منفی به صورت اعداد باینری که برای بدست آوردن صفر با یک عدد مثبت با همان اندازه جمع می‌شوند، نمایش داده می‌شوند. شما با گرفتن مکمل یک (معکوس کردن بیت‌ها) یک عدد مثبت و سپس اضافه کردن یک واحد به آن، عدد مکمل دو منفی را محاسبه می‌کنید. سیستم اعداد مکمل دو به شما این امکان را می‌دهد که به جای انجام عمل تفریق با جمع کردن دو عدد آن‌ها را از هم کنید. دامنه تغییرات اعداد مکمل دو به صورت رابطه (۱) قابل نمایش است.

$$2^{N-1} : 2^{N-1}-1$$

رابطه (۱)

راه دیگر برای بدست آوردن مقدار مکمل دو یک عدد باینری، از سمت راست به چپ به این صورت است که تمامی بیت‌ها تا قبل از اولین بیت '1' را دست نخورده نگه می‌داریم و سپس بیت‌های باقیمانده را معکوس می‌کنیم.

محاسبات ممیز ثابت

چندین روش برای نشان داده فرمت‌های ممیز ثابت استفاده می‌شود، فرمت مرسوم نمایش بیت‌های صحیح و اعشاری در یک عدد ممیز ثابت به صورت نمایش x,y است که در آن x تعداد بیت‌های صحیح و y تعداد بیت‌های اعشاری را نشان می‌دهد. به عنوان مثال عددی با فرمت 8,8 دارای ۸ بیت صحیح و ۸ بیت اعشار است، در حالی که فرمت 16,0 نمایانگر اختصاص ۱۶ بیت صحیح و صفر بیت اعشار است. در بسیاری از موارد، طراح تعداد بیت‌های بخش صحیح و بخش اعشاری را در زمان طراحی را تعیین می‌کند، فرایند ممیز ثابت کردن عموما بر اساس یک الگوریتم ممیز شناور صورت می‌پذیرد و در آن ما به دنبال تبدیل یک الگوریتم ممیز شناور به الگوریتم ممیز ثابت هستیم.

فرمت دیگری نیز برای نمایش اعداد ممیز ثابت وجود دارد که در آن علامت دار بودن یا بدون علامت بودن نیز نشان داده می‌شود. این فرمت به صورت Uxxyy برای اعداد بدون علامت و Qxxyy برای اعداد علامت دار نمایش داده می‌شود. در این الگو xx بیانگر تعداد بیت‌های اختصاص داده شده به متغیر ممیز ثابت و yy معرف تعداد بیت‌های اعشاری آن است. به عنوان مثال متغییری با فرمت U1608، عددی بدون علامت با ۸ بیت صحیح و ۸ بیت اعشار است و عددی با فرمت Q1600 دارای ۱۶ بیت صحیح و صفر بیت اعشار و البته علامت دار است. در طول این مقاله از این شیوه برای نمایش استفاده خواهیم کرد.

به لطف انعطاف‌پذیری FPGA ها، ما می‌توانیم عدد ممیز ثابت را با هر طول بیتی نشان دهیم. تعداد بیت‌های بخش صحیح بستگی به اندازه بزرگترین عدد صحیح مورد نیاز در محاسبات دارد. در حالی که تعداد بیت‌های بخش اعشاری به صحت و دقت مورد نیاز برای محاسبات وابسته است. برای تعیین تعداد بیت‌های صحیح مورد نیاز معمولاً از رابطه (۲) استفاده می‌شود.

$${Integer \hspace{4 pt} Bit \hspace{4 pt} Required}= ceil(log_2(max(Integer)))$$

رابطه (۲)

برای مثال تعداد بیت‌های مورد نیاز برای نمایش بخش صحیح اعداد بین صفر تا ۴۲۳ با توجه به رابطه (۲) به صورت زیر محاسبه می‌شود.

$$9 =ceil(log_2(423))$$

رابطه (۳)

این بدان معناست که ما به ۹ بیت برای نمایش بخش صحیح نیاز خواهیم داشت. به این ترتیب دامنه تغییرات قابل نمایش بین صفر تا ۵۱۱ خواهد بود. نمایش عدد ۴۲۳ با استفاده از ۱۶ بیت امکان اختصاص ۷ بیت برای نمایش بخش اعشاری را فراهم می‌آورد. دقتی که این شیوه نمایش قادر به نمایش آن است، با توجه به رابطه (۴) بدست می‌آید.

$$Accuracy={Actual \hspace{4 pt} Value – {FPGA \hspace{4 pt} Value} \over 2^{Fractional \hspace{4 pt} Bit}}$$

رابطه (۴)

ما می‌توانیم دقت اعداد ممیز ثابت را با افزایش تعداد بیت‌های بخش اعشاری افزایش دهیم. در طول طراحی، زمان‌هایی وجود دارد که طراح ترجیح می‌دهد تنها مقادیر اعشاری را ذخیره کند‍ (مثلا دخیره عددی با فرمت 0,16 یا U1616). با توجه به سایز عدد ممکن است تمایل داشته باشیم که آن را مقیاس‌بندی کنیم و در مقیاس جدیدی نمایش بدهیم. از طرفی مقیاس‌بندی با فاکتور 2¹⁶ ممکن است به عددی منتهی شود که هنوز از دقت آن رضایت نداریم. در چنین مواردی ما می‌توانیم عدد مدنظر را در توانی از ۲ ضرب کنیم. در حالی که حاصل همچنان قابلیت نمایش درون یک کلمه ۱۶ بیتی را دارد. این مقیاس‌بندی در گام‌های بعدی در طول پیاده‌سازی قابل حذف است.

به عنوان مثال، برای نمایش عدد ^4-10×1.373291001563 در یک کلمه ۱۶ بیتی، در اولین گام باید این عدد را در عدد 2¹⁶ ضرب کنیم.

$$65536 \times 1.45309806319 \times 10^{-4}= 9.523023$$

$$floor(9.523023)=9$$

رابطه (۵)

اینجا باید بخش صحیح پاسخ یعنی مقدار ۹ را در نظر بگیریم (معادل دستور floor در Matlab). اینکار معادل با ذخیره عددی به صورت زیر است:

$$1.373291001563 \times 10^{-4}  ({9 \over 65536})$$

رابطه (۶)

احتمالاً متوجه شده‌اید که دو عدد محاسبه شده با هم متفاوت هستند. این تفاوت بین عدد مورد انتظار و عدد ذخیره شده کاملا ذاتی است و در نهایت منجربه ایجاد خطای غیرقابل پذیرش در خروجی می‌شود. برای بهتر کردن شرایط و بالا بردن دقت ما می‌توانیم از فاکتور 2²⁸ برای مقیاس‌بندی عدد استفاده کنیم. به این ترتیب عدد نهایی مقداری بین ۳۲۷۶۸ تا ۶۵۵۳۶ خواهد داشت. علاوه بر این همچنان امکان نمایش آن در ۱۶ بیت وجود دارد. نکته جالب اینجاست که استفاده از فاکتور 2²⁸ و ضرب آن در عدد ^4-10×1.373291001563 مقداری به مراتب دقیق تر را به همراه دارد در حالی که همچنان ۱۶ بیت برای نمایش عدد مقیاس‌بندی شده کفایت می‌کند. به رابطه (۷) دقت کنید.

$$268435456 \times 1.45309806319 \times 10^{-4}= 39006.3041205$$

رابطه (۷)

در چنین شرایطی مقدار ذخیره شده قابلیت شرکت محاسبات و تولید پاسخ‌های بسیار دقیقی را فراهم می‌آورد فرض کنید عدد ^4-10×1.373291001563 با استفاده از فاکتور مقیاس‌بندی 2²⁸ در یک رجیستر ۲۸ بیتی ذخیره شده است. در این صورت محاسبه حاصل ضرب یک عدد ۱۶ بیتی با فرمت U1612 با عدد فوق که فرمت U2828 دارد، پاسخی با فرمت U4440 تولید می‌کند. این نتیجه می‌تواند با دقت مناسبی در یک رجیستر ۳۲ بیتی ذخیره شود.

نتیجه اینکه برای دستیابی به دقت بالاتر در محاسبات می‌توان از فرمت‌های ممیز ثابت مقیاس‌بندی شده که قابلیت ذخیره کردن تعداد بیشتر بیت اعشار را دارند استفاده کرد. در ادامه بشتر در این رابطه صحبت خواهیم کرد.

قوانین محاسبات ممیز ثابت

جمع، تفریق یا تقسیم

برای جمع، تفریق یا تقسیم نقطه اعشار دو عدد شرکت کننده در محاسبه باید با یکدیگر تراز شوند. پس تنها در صورتی می‌توان عددی با فرمت Uxx08 را با عدد ممیز ثابت دیگری جمع، تفریق و یا تقسیم کرد که عدد دیگر نیز دارای فرمت ممیز ثابت Uxx08 باشد. برای اجرای عملیات ریاضی روی اعدادی که فرمت نمایش متفاوت Uxxyy دارند، ابتدا باید نقطه اعشار دو عدد باهم تراز شوند، هیچ استثنایی هم وجود ندارد.

برای جمع، تفریق یا تقسیم نقطه اعشار دو عدد شرکت کننده در محاسبه باید با یکدیگر تراز شوند.

برای تراز کردن نقطه اعشار اعداد دو انتخاب وجود دارد:

• ضرب عدد بزرگتر در ضریب 2X یا
• تقسیم عدد کوچکتر بر 2X

به بیان ساده‌تر عدد با تعداد بیت صحیح بیشتر را در 2X و عدد با تعداد بیت صحیح کمتر را در 1/2X ضرب می کنیم. تقسیم بر عدد 2X معادل شیفت به راست است و در نتیجه از دقت عدد می‌کاهد. به این ترتیب ممکن است دقت نهایی محاسبات در محدوده قابل پذیرش قرار نگیرد و خطا افزایش یابد. همانطور که اشاره شد ضرب یا تقسیم در مضارب ۲ تنها با شیفت اعداد به ترتیب به سمت چپ و راست انجام می‌شود. از این رو برای تراز کردن نقطه اعشار و تغییر مقیاس اعداد نیاز به محاسبه ضرب نداریم. برای جمع دو عدد ممیز ثابت با فرمت‌های U1608 و U1607 بهتر است عدد دوم یک بیت به سمت چپ شیفت داده بشود. در صورتی که از دست رفتن بیت کم ارزش در عدد اول روی دقت محاسبات تاثیرگذار نباشد. می‌توان عدد اول را یک بیت به سمت راست شیفت داد.

برای مثال، فرض کنیم قصد داریم عدد ۲۳۴.۵۸ و عدد ۳۱۲.۷۳۲ را با هم جمع کنیم، این دو عدد به ترتیب با فرمت U1608 و U1607 درون FPGA ذخیره شده‌اند. اولین گام، تعیین دقیق ۱۶ بیتی است که قرار است با هم جمع کنیم.

$$234.58 \times 28 = 60052.48$$

$$312.732 \times 27 = 40029.69$$

رابطه (۸)

اعدادی که قرار است با هم جمع شوند ۶۰۰۵۲ و ۴۰۰۲۹ هستند. توجه داشته باشید که قبل از محاسبه حاصل جمع ابتدا باید نقطه اعشار آن ها را با هم تراز کنیم. پس عدد بزرگتر را به عنوان عدد مرجع در نظر می‌گیریم. لازم است برای تراز کردن نقطه اعشار عدد کوچکتر را در عدد ۲ ضرب کنیم. یعنی فاکتور مقیاس‌بندی را 2¹ در نظر بگیرم.

$$40029 \times 2 = 80058$$

رابطه (۹)

در ادامه محاسبه حاصل جمع به صورت زیر قابل انجام است

$$80058 + 60052 = 140110$$

رابطه (۱۰)

نمایش U1810 عدد حاصل برابر با ۵۴۷.۳۰۴۶۸۷۵  است یعنی در نهایت پاسخ را بر فاکتور 2⁸ تقسیم کردیم.

ضرب

در زمان محاسبه حاصل ضرب دو عدد، نیازی به تراز کردن نقاط اعشار نداریم. زیرا تعداد بیت‌های حاصل از ضرب دو عدد با جمع کردن تعداد بیت‌های آن دو محاسبه می‌شود. به بیان ساده‌تر بیت‌های صحیح باهم و بیت‌های اعشار باهم جمع می‌شوند. اگر فرض کنیم x1 و x2 تعدا بیت‌های صحیح و y1 و y2 تعداد بیت های اعشاری دو عدد هستند، برای پاسخ داریم: x1 + x2, y1 + y2.

در زمان محاسبه حاصل ضرب دو عدد، نیازی به تراز کردن نقاط اعشار نداریم.

به عنوان مثال حاصل ضرب دو عدد ۱۶ بیتی که با فرمت‌های U1602 و U1606 نمایش داده شده‌اند یک عدد ۳۲ بیتی با ۲۴ بیت صحیح و ۸ بیت اعشار است.

در حالت کلی ضرب در یک عدد کسری که فقط بخش اعشاری دارد معادل تقسیم بر معکوس آن عدد است. این یعنی عملگر تقسیم با عملگر ضرب قابل جایگزینی است. این رویکرد باعث کاهش چشمگیر پیچیدگی‌های طراحی می‌شود. برای مثال برای تقسیم عدد ۳۱۲.۷۳۲ که با فرمت U1607 نمایش داده شده است (۴۰۰۲۹) بر عدد ۱۵، اولین گام محاسبه معکوس عدد ۱۵ است.

$${1 \over 15} = 0.666’$$

رابطه (۱۱)

در ادامه مقدار محاسبه شده باید برای قرار گرفتن در یک کلمه ۱۶ بیتی مقیاس‌بندی شود.

$$65536 \times 0.06666 = 4369$$

رابطه (۱۲)

این مقیاس‌بندی باعث می‌شود پاسخ نهایی در قالب فرمت ممیز ثابت U3223 تولید شود. یعنی ۹ بیت صحیح و ۲۳ بیت اعشار.

$$4369 \times 40029 = 174886701$$

رابطه (۱۳)

پاسخ نهایی این تقسیم برابر است با

$${174886701 \over 8388608} = 20.8481193781$$

رابطه (۱۴)

با توجه به اینکه پاسخ مطلوب ۲۰.۸۴۸۸ است، اگر پاسخ نهایی به اندازه کافی دقیق نیست. نیاز داریم فاکتور مقیاس‌بندی برای محاسبه معکوس عدد ۱۵ را بزرگتر بکنیم. در نتیجه زمانی که نیاز به تقسیم بر یک یک عدد ثابت داشتید، هرگز اینکار را انجام ندهید و تقسیم را با ضرب جایگزین کنید.

مطلبی که مطالعه کردید قسمت اول از مقاله آموزشی محاسبات ریاضی در FPGA بود، ادامه این مطلب را در قسمت دوم مقاله مطالعه بفرمایید.

با اقتباس از Xcell Journal