پیاده‌سازی فیلتر میانگین‌گیر متحرک در FPGA

مقدمه

فیلتر میانگین‌گیر متحرک یا فیلتر moving average یکی از ساده‌ترین انواع فیلترهای دیجیتال است. این فیلتر برای مواردی همچون حذف نویز یا هموار کردن سیگنال‌ها در حوزه زمان بکار گرفته می‌شود.

در این آموزش از پایگاه دانش هگزالینکس قصد داریم الگوی پیاده‌سازی بهینه یک فیلتر میانگین‌گیر متحرک را به شما توضیح دهیم. در ابتدا با استفاده از یک الگوی بازگشتی حجم محاسبات را کاهش می‌دهیم و سپس با ارائه کدهای HDL نحوه کنترل رشد بیت را بررسی می‌کنیم. پس تا انتها با ما همراه باشید.

فیلتر میانگین‌گیر متحرک

مشخصات فیلتر میانگین‌گیر با توجه به کاربرد مد نظر متفاوت است. اما به طور کلی با استفاده از رابطه (۱) توصیف می‌شود. در این فیلتر برای هر نمونه داده در ورودی، نیاز داریم یکبار کل محاسبه را انجام دهیم.

$$y(k)=\frac{1}{N}\sum_{i=k}^{N+k+1}x_{i}$$

رابطه (۱)

به بیان ساده، مقدار y در هر لحظه با متوسط گیری روی تعدادی از ورودی‌های متوالی محاسبه می‌شود. تعداد این ورودی‌ها با N نمایش داده می‌شود و طول فیلتر نامیده می‌شود. برای N=4 مقدار y با میانگین‌گیری روی ۴ ورودی آخر x محاسبه می‌شود. این مسأله در روابط (۲) نشان داده شده است.

$$y(0)=\frac{1}{N} (x_0+x_1+x_2+x_3)$$

$$y(1)=\frac{1}{N} (x_1+x_2+x_3+x_4)$$

$$y(2)=\frac{1}{N} (x_2+x_3+x_4+x_5)$$

رابطه (۲)

ملاحظات پیاده‌سازی

برای شروع کار پیاده‌سازی ابتدا از عدد ۴ صرف نظر می‌کنیم و روی محاسبه جمع تمرکز می‌کنیم. فرض می‌کنیم برای (2)y داشته باشیم:

$$y(2)= (x_2+x_3+x_4+x_5)$$

$$y(2)=(y(1)+x_5-x_1)$$

رابطه (۳)

بازنویسی رابطه (۳) و محاسبه با استفاده ازیک روش مرسوم در پیاده‌سازی فیلتر میانگین‌گیر متحرک است. به این شکل از محاسبه در اصطلاح محاسبه بازگشتی یا recursive گفته می‌شود. از این رو رابطه (۱) را می‌توان بصورت رابطه (۴) بازنویسی کرد.

$$y(k)=\frac{1}{N} (y({k-1})+x_{n+N}+x_n)$$

رابطه (۴)

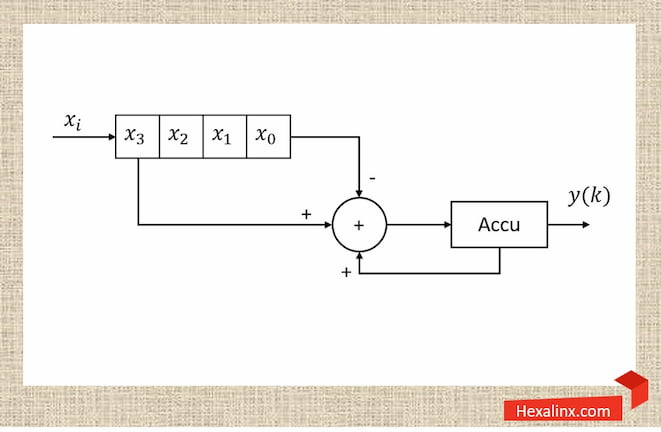
با در نظر گرفتن رابطه (۳) معماری فیلتر میانگین‌گیر به شدت ساده می‌شود. در شکل (۱) این معماری برای N=4 نشان داده شده است. در این معماری برای محاسبه هر مقدار جدید y کافی است اولین نمونه ورودی به بلوک فیلتر را با مقدار قبلی y جمع کنیم و قدیمی‌ترین مقدار ذخیره شده یا همان نمونه خروجی را از حاصل جمع کم کنیم. در معماری فوق تأثیر پارامتر N در نظر گرفته نشده است. در مورد چگونگی انجام عمل تقسیم در FPGA می‌توان راه حل متفاوتی را در نظر گرفت که به آن خواهیم پرداخت.

نکته اول

نکته اول در پیاده‌سازی مربوط به محاسبه رشد بیت است. جمع‌های پیاپی باعث افزایش تعداد بیت‌های حاصل جمع می‌شود. به عنوان مثال برای ذخیره کردن حاصل جمع دو عدد ۸ بیتی در بدترین حالت نیاز به ۹ بیت خواهیم داشت. در حالت کلی تعداد بیت‌های اضافی مورد نیاز برای انجام جمع‌های پیاپی از رابطه ‏(N‏)Log₂ محاسبه می‌شود. عدد N نشان دهنده تعداد مقادیری است که باید با هم جمع بشوند. در مثال ما برای N=4 رشد بیت برابر ۲ خواهد بود. به بیان ساده‌تر برای جلوگیری از سرریز شدن هنگام جمع ۴ عدد نیاز به استفاده از ۲ بیت اضافه داریم. محاسبه رشد بیت و کنترل سرریز یکی از مسائلی است که باید به شکل ویژه در الگوریتم‌های ریاضی مد نظر قرار داده شود.

نکته دوم

نکته دوم مربوط به ذخیره‌سازی ورودی‌های فیلتر است. برای اینکه به مقادیر ورودی و تأخیر یافته‌های آن دسترسی داشته باشیم باید در ساده ترین حالت از یک شیفت رجیستر استفاده کنیم. پس باید کدنویسی مناسب برای پیاده سازی شیفت رجیستری به طول N را انجام دهیم.

نکته سوم

نکته سوم مربوط به پیاده‌سازی عملگر تقسیم در رابطه (۱) است. به طور کلی در پیاده‌سازی‌های مبتنی بر FPGA تا حد امکان از پیاده‌سازی تقسیم خودداری می‌کنیم و معمولاً برای آن جایگزین مناسبی پیدا می‌کنیم. با توجه به ماهیت پیاده‌سازی ممکن است انتخاب ما برای محاسبه تقسیم متفاوت باشد. در پیاده‌سازی فیلتر میانگین‌گیر متحرک ما از ضرب به جای تقسیم استفاده می‌کنیم. یعنی به جای تقسیم حاصل جمع بر N ، حاصلضرب پاسخ در N‏/1 را محاسبه‌ می‌کنیم. برای اینکار معمولا مقدار N‏/1 در Matlab‌ محاسبه و در داخل کد ذخیره می‌شود. (چگونه؟)

در پیاده سازی شیفت رجیستر نباید از ریست استفاده شود، چون در این صورت امکان فراخوانی شیفت رجیسترهای درون LUT وحود نخواهد داشت.

نکات تکمیلی

پیش از بررسی کدهای HDL لازم است نکات زیر را مد نظر قرار دهیم.

• اگر N مضربی از ۲ باشد می‌توان به جای تقسیم از شیفت به راست استفاده کرد. اگر مضربی از ۲ نباشد باید به جای تقسیم از ضرب استفاده کرد.
• اگر N خیلی بزرگ باشد استفاده از شیفت رجیستر چندان انتخاب مناسبی نیست. در این حالت بهتر است از حافظه‌های توزیع شده و یا بلوکی برای دخیره مقادیر x استفاده کرد.
• اگر عرض بیت داده‌های ورودی و خروجی کم باشد می‌توان مقدار حاصل جمع را با استفاده از LUT ها پیاده‌سازی کرد. اما اگر با عرض بیت‌های بالا سرو کار داریم، بهتر است حتما از بلوک‌های ضرب‌کننده DSP‌ استفاده شود.
• برای دستیابی به حداکثر کارایی می‌توان سیگنال ورودی به ماژول را رجیستر کرد. در این صورت تاخیر کلی مدار یک کلاک افزایش پیدا می‌کند.
• اولین خروجی معتبر زمانی قابل محاسبه است که حداقل N ورودی در داخل شیفت رجیستر یا حافظه ذخیره شده باشند.

پیاده‌سازی

پیاده‌‌سازی فیلتر به صورت کاملا انعطاف پذیر انجام شده است. کافی است طول فیلتر، عرض بیت ورودی و عرض بیت خروجی به صورت پارامتریک تعیین شوند. در ادامه کد VHDL نهایی با توجه به معماری پیشنهادی ارائه شده است. در این کد مقدار N برابر با ۴ در نظر گرفته شده است. به این ترتیب، بدون نیاز به پیاده‌سازی تقسیم تنها با استفاده از عملیات شیفت به راست تقسیم صوت پذیرفته است.

-- copyright 2019 Hexalinx.com

library ieee;
use ieee.std_logic_1164.all;
use ieee.numeric_std.all;

entity moving_average is
generic (
    WORD_LEN                   : integer := 8;
    FILTER_SIZE                : integer := 4;
    LOG2_FILTER_SIZE           : integer := 2);
port (
    Clk                        : in  std_logic;
    Rst                        : in  std_logic;
    -- input
    Valid_i                    : in  std_logic;
    Data_i                     : in  std_logic_vector(WORD_LEN-1 downto 0);
    -- output
    Valid_o                    : out std_logic;
    Data_o                     : out std_logic_vector(WORD_LEN-1 downto 0));
end moving_average;

architecture behavioral of moving_average is

    type MOVING_AVERAGE_TYPE is array (0 to 2**LOG2_FILTER_SIZE-1) of 
    signed(WORD_LEN-1 downto 0);

    signal moving_average_srl  : MOVING_AVERAGE_TYPE;
    signal acc_r1              : signed(WORD_LEN+LOG2_FILTER_SIZE-1 downto 0);  -- average accumulator
    signal Valid_r1            : std_logic;

begin

    p_average: 
    process(Clk)
    begin
        if rising_edge(Clk) then

            if(Rst='1') then
                Valid_r1           <= Valid_i;
                acc_r1             <= (others=>'0');
            elsif (Valid_i = '1') then
                moving_average_srl <= signed(Data_i) & moving_average_srl(0 to moving_average_srl'length-2);     -- shift right
                acc_r1             <= acc_r1 + signed(Data_i) - moving_average_srl(moving_average_srl'length-1); -- accumulate
            end if;

            Valid_r1  <= Valid_i;
            Valid_o   <= Valid_r1;  
            Data_o    <= std_logic_vector(acc_r1(WORD_LEN + LOG2_FILTER_SIZE-1 downto LOG2_FILTER_SIZE));  -- divide by 2^LOG2_FILTER_SIZE
      
        end if;
    end process p_average;

end behavioral;

جمع بندی

در این آموزش پیاده‌سازی کاملا بهینه یک فیلتر میانگین‌گیر متحرک را با هم مرور کردیم. سپس با نحوه پیاده‌سازی معماری‌های بازگشتی آشنا شدیم. در نهایت روش محاسبه رشد بیت برای جمع کننده انباره را فراگرفتیم. برای پیاده‌سازی فیلترهای پیچیده‌تر نیز از مفاهیم مشابه استفاده می‌شود. مدارات کنترلی در این فیلترها محدود هستند و معمولا نیازی به ریست کردن مقادیر میانی ذخیره شده در فیلتر وجود ندارد.