یادآوری
در قسمت اول از مقاله در رابطه با شیوه نمایش اعداد ممیز ثابت و قوانین استفاده از آنها در محاسبات ریاضی صحبت کردیم. در قسمت دوم قصد داریم کمی دقیقتر ملاحظات پیادهسازی را باهم مرور کنیم. ابتدا مسأله سرریز و شیوه کنترل آن را بررسی میکنیم و در ادامه با یک مثال قوانینی را که با هم یادگرفتیم، بکار میگیریم. پیادهسازی سطح رجیستر و کدهای HDL نیز در انتها حضورتان تقدیم میگردد.
اگر هنوز قسمت اول را مطالعه نکردهاید از لینک زیر استفاده کنید و بعد از مطالعه قسمت اول با ما همراه شوید.
مشکل سرریز
هرگاه در حال پیادهسازی یک الگوریتم ریاضی هستیم. حتما باید به این نکته دقت کنیم که عرض بیت پاسخ نهایی نباید از عرض (طول) بیت در نظر گرفته شده برای آن فراتر رود. در غیر این صورت اصطلاحاً سرریز رخ میدهد. در صورت بروز سرریز پاسخ نامعتبر میشود و با ارزشترین بیت از دست میرود. یک مثال ساده از وقوع سرریز جمع دو عدد ۱۶ بیتی با مقدار ۶۵۵۳۵ است. در این حالت ذخیره پاسخ در یک رجیستر ۱۶ بیتی سرریز به همراه دارد.
$$65535 + 65535 = 131070$$
رابطه (۱۵)
در صورت بروز سرریز پاسخ نامعتبر میشود و با ارزشترین بیت از دست میرود
بعد از محاسبه حاصل جمع فوق و ذخیره آن در رجیستر ۱۶ بیتی مقدار ذخیره شده برابر با ۶۵۵۳۴ خواهد بود. که کاملاً اشتباه است. سادهترین راه برای جلوگیری از سرریز محاسبه رشد بیت پاسخ بعد از انجام هر عملیات ریاضی و در نهایت اختصاص بیتهای کافی به پاسخ است.
$${Bit \hspace{4 pt} Required}= ceil(log_2(max(Answer)))$$
رابطه (۱۶)
اگر فرض کنیم که در حال پیادهسازی یک تابع میانگینگیر روی پنجاه عدد ۱۶ بیتی هستیم. عرض بیت نهایی مورد نیاز برای ذخیره پاسخ با توجه به رابطه (۱۶) محاسبه میشود. بزرگترین مقدار ممکن برای محاسبه حاصل جمع ۵۰ عدد به صورت زیر محاسبه میشود.
$$50\times 65535 = 3276750$$
رابطه (۱۷)
با استفاده از رابطه (۱۶)، متوجه خواهیم شد که برای جلوگیری از سرریز نیاز به استفاده از ۲۲ بیت داریم. از سوی دیگر باید به این نکته توجه داشته باشیم که قرار است در انجام محاسبات از اعداد علامت دار استفاده کنیم و در صورت منفی بودن اعداد بازهم باید ملاحظات لازم برای ممناعت از سرریز را در نظر بگیریم. استفاده از میانگینگیر قبلی برای محاسبه میانگین ده عدد علامت دار، احتمالا پاسخی ۱۶ بیتی به همراه دارد. در روابط (۱۷) و (۱۸) ما در بدبینانه ترین حالت حاصل جمع را محاسبه کردیم. در نهایت برای دستیابی به پاسخ نهایی باید مقادیر محاسبه شده را به ترتیب بر ۵۰ و ۱۰ تقسیم کنیم تا مقدار میانگین را به دست آوریم.
$$10 \times {(-32768)} = -327680$$
$$6554 \times{(-327680)} = -2147614720$$
رابطه (۱۸)
با توجه به نکاتی که تا کنون یادگرفتیم، میدانیم که برای محاسبه میانگین، محاسبه حاصل ضرب عدد ۳۲۷۶۸- در معکوس عدد ۱۰ سادهتر از اجرای عملیات تقسیم است. با مقیاسبندی عدد 1/10 با فاکتور 216 مقدار ۶۵۵۴ بدست میآید که از آن میتوان مطابق با رابطه (۱۸) برای محاسبه میانگین استفاده کرد.
اگر عدد بدست آمده از رابطه (۱۸) را بر فاکتور 216 تقسیم کنیم عدد حاصل برابر با ۳۲۷۷۰- میشود، کاملاً واضح است که این عدد در یک رجیستر ۱۶ بیتی قابل نمایش نیست. این یعنی سرریز رخ داده است. بنابراین همواره باید در زمان طراحی محاسبات ممیز ثابت احتمال وقوع سرریز به صورت کامل بررسی شود و متناسب با آن چاره اندیشی شود.
به طور کلی رشد بیت حاصل از جمعهای پیاپی اعداد علامت دار با استفاده از رابطه (۱۹) محاسبه می شود.
$$Bit \hspace {4 pt} Growth =ceil(log_2(Number\hspace {4 pt} of\hspace {4 pt} Sum))$$
رابطه (۱۹)
در زمان طراحی محاسبات ممیز ثابت احتمال وقوع سرریز به صورت کامل بررسی شود و متناسب با آن چاره اندیشی شود.
از تعداد زیاد روابط ارائه شده در این بخش ناامید نشوید، تقریباً همه روابط بیانگر یک مفهوم واحد هستند و با چندبار تمرین کاملاً به خاطر سپرده میشوند. در ادامه روش استفاده عملی از این روابط را در یک مثال واقعی فراخواهید گرفت.
پیادهسازی یک تابع تبدیل
فرض کنیم شما به عنوان یک طراح نیاز دارید ماژولی برای پیادهسازی یک تابع تبدیل طراحی کنید. این تابع برای تبدیل فشار اتمفسر برحسب میلی بار به ارتفاع برحسب متر بکار میرود.
$$-0.0088x^2 + 1.7673x + 131.29$$
رابطه (۲۰)
گام اول
دامنه تغییرات ورودی بین صفر تا 10mbar با رزولوشن 0.1mbar فرض شده است. خروجی ماژول نیز دقتی معادل 0.01m± نیاز دارد. با توجه به اینکه توضیحات ارائه شده به همراه تابع تبدیل اطلاعاتی در رابطه با مقیاسبندی و فرمت ممیز ثابت اعداد ارائه نمیدهد، شما میتوانید با استفاده از رابطه (۲۱) روی این موضوع تصمیم گیری کنید.
بنابراین، به منظور دستیابی به حداکثر دقت شما باید فرمت داده ورودی را به صورت U1612 با ۴ بیت صحیح و ۱۲ بیت اعشار در نظر بگیرید. دقت شود که در اینجا ورودی بدون علامت فرض شده است، در صورت علامت دار بودن باید از ۵ بیت صحیح استفاده می کردیم.
$$4 =ceil(log_2(10))$$
رابطه (۲۱)
گام دوم
گام بعدی در محاسبه این ماژول استفاده از نرم افزارهای ریاضی همچون Matlab و یا Excel برای محاسبه پاسخ مطلوب تابع تبدیل به ازای تمامی مقادیر ورودی است. این کار باید با استفاده از مقادیر مقیاسبندی نشده صورت بپذیرد. اگر دامنه تغییرات ورودی خیلی وسیع باشد، باید به اندازه کافی ورودی متفاوت انتخاب شود تا نتایج محاسبه شده در خروجی قابل اطمینان باشند. (بعنی مطمئن شوید تمامی حالات را در نظر گرفته شده است). برای این مثال شما میتوانید ۱۰۰ نمونه از ورودی انتخاب کنید و به عنوان مدلی از کلیه ورودیهای ممکن، دامنه تغییرات خروجی را محاسبه کنید. چند نمونه اول در جدول (۱) نشان داده شده است.
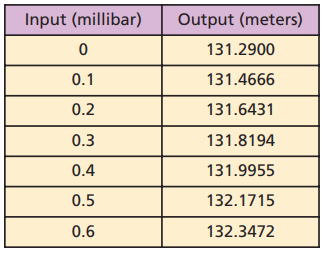
گام سوم
بعد از اتمام فراید محاسبه مقادیر خروجی، گام سوم انتخاب یک فاکتور مناسب برای مقیاسبندی مقادیر ثابت موجود در تابع تبدیل است. در ادامه خروجی تابع تبدیل باید با استفاده از این مقادیر مقیاسبندی شده مجددا محاسبه شود. بازهم برای حصول اطمینان از دقت محاسبات مجبوریم هر کدام از مقادیر ثابت در تابع تبدیل را با یک فرمت متفاوت مقیاسبندی کنیم.
فاکتور مقیاسبندی برای اولین مقدار ثابت یعنی A با توجه به رابطه (۲۲) به دست میآید.
$$8 =ceil(log_2(131.29))$$
رابطه (۲۲)
دومین مقدار ثابت تابع تبدیل یعنی B با استفاده از مقدار محاسبه شده در رابطه (۲۳) تعیین میگردد. در اینحا فقط نیاز به یک بیت صحیح برای نمایش B داریم.
$$1 =ceil(log_2(1.7673))$$
رابطه (۲۳)
در نهایت فاکتور مقیاسبندی برای آخرین مقدار ثابت تابع تبدیل یعنی متغیر C برابر با 216 در نظر گرفته میشود. دلیل آن هم کوچک بودن و کاملا اعشاری بودن مقدار C است.
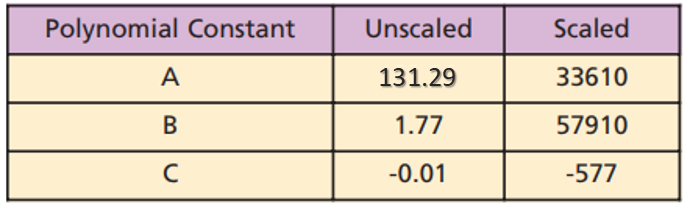
این فاکتورهای مقیاسبندی شده به شما اجازه میدهند تا مقادیر خروجی را به صورت مقیاسبندی شده مطابق با جدول (۳) محاسبه کنید. نتیجه هر گام از محاسبات، پاسخهایی را به همراه خواهد داشت که برای ذخیره آنها به بیش از ۱۶ بیت نیاز داریم.
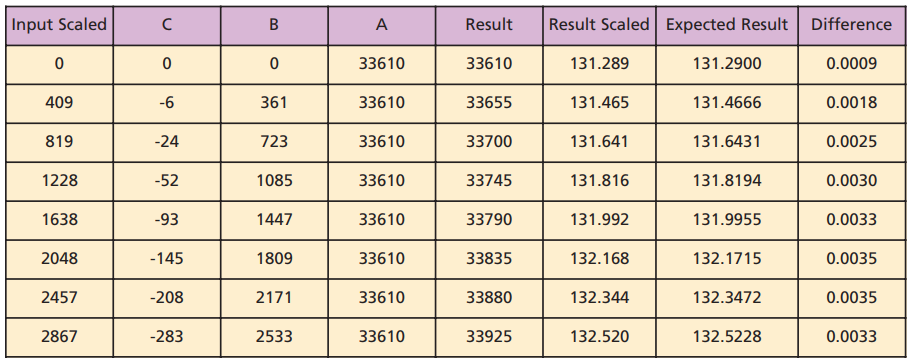
محاسبه حاصل ضرب
محاسبه متغیر Cx2 منجربه تولید یک پاسخی ۳۲ بیتی میشود، یعنی U1612+U1612=U3224 . سپس این عدد در مقدار ثابت C ضرب میشود و پاسخی ۴۸ بیتی تولید میکند. فرمت پاسخ تولید شده بدون شک U4840 خواهد بود. برای دستیابی به دقت مورد انتظار در این مساله استفاده از ۴۰ بیت اعشاری کمی بیش از حد سخت گیرانه به نظر میرسد. بنابراین برای برقراری یک مصالحه بین منابع مصرفی و دقت، پاسخ به دست آمده را ۳۲ بیت به سمت راست شیفت میدهیم یا به بیان ساده تر پاسخ را بر فاکتور 232 تقسیم میکنیم. به این ترتیب عرض بیت خروجی در این گام به ۱۶ بیت کاهش مییابد. ۸ بیت آن برای نمایش بخش صحیح و ۸ بیت کم ارزش آن برای نمایش بخش اعشار قابل استفاده است. فرمت خروجی در این حالت U1608 خواهد بود.
مشابهاً برای بدست آوردن مقدار Bx محاسبات و سپس کاهش عرض بیت به شکلی که برای Cx2 انجام شد، صورت میپذیرد. آیا میتوانید با استفاده از قلم و کاغذ فرمت خروجی Bx را محاسبه کنید؟ فرمت خروجی بعد از کاهش عرض بیت U1611 خواهد بود.
محاسبه حاصل جمع
در ادامه باید حاصل جمع متغیرهای Cx2 و Bx و A را محاسبه کنیم. برای دستیابی به پاسخ صحیح باید ابتدا نقاط اعشار را زیر هم تراز کنیم. این کار با شیفت متغیرهای A و Cx2 به سمت چپ برای ساخت ۱۱ بیت اعشار و یا شیفت به سمت چپ متغیر Bx برای ساخت ۸ بیت اعشار امکان پذیر است. اما سوال اینجاست کدام یک بهتر است؟ با شیفت به سمت راست متغییر Cx2 و A فرمت Uxx11 خواهند داشت و در صورت شیفت به راست متغیر Bx فرمت Uxx08 خواهد داشت.
در این مثال ما از شیفت به سمت راست و در نتیجه کاهش تعداد بیتهای اعشار به ۸ بیت استفاده میکنیم. برای این کار کافی است مقدار Bx را بر 23 تقسیم کنیم تا فرمت آن U1608 شود. با این رویکرد حداقل تعداد شیفت انجام میشود، و در منابع مصرفی روی تراشه صرفه جویی میشود. توجه شود که در صورتی که استفاده از ۸ بیت برای دستیابی به دقت مطلوب کفایت نکند آنگاه شما مجبور هستید با شیفت به چپ مقادیر A و Cx2 تعداد بیتهای اعشار را افزایش دهید.
محاسبه خطای پاسخ
در انتهای کار پاسخ نهایی با استفاده از فاکتور 28 محاسبه میشود. شما میتوانید با حذف اثر این مقیاس و کوچک کردن آن نتیجه نهایی را با مقادیر مقیاسبندی نشده که در ابتدا محاسبه کرده بودید، مقایسه کنید. تفاوت میان نتایج به دست آمده با نتایج مطلوب مورد انتظار دقت محاسبات را تعیین میکند. با استفاده از توابع min و max در Matlab به سادگی میتوان خطای حاصل از محاسبات را به ازای تمامی مقادیر ورودی محاسبه کرد.
بعد از مقایسه درخواهید یافت که شما به دقت مطلوب دست یافتهاید و فرایند مقیاسبندی و ممیز ثابت کردن تابع تبدیل مطابق انتظار پیش رفته است. خب حالا نویت به پیادهسازی سختافزاری، کدنویسی HDL و در ادامه شبیهسازی آن میرسد. برای سادگی کار و تسهیل فرایند صحه گذاری طراح پیشنهاد میشود از مقادیر مورد استفاده برای تعیین فرمتهای ممیزثابت به عنوان مقادیر ورودی در testbench استفاده شود. به این ترتیب ارزیابی صحت عملکرد پیادهسازی تابع در سطح رجیستر سادهتر میشود.
پیاده سازی سطح رجیستر
مثال زیر با استفاده از محاسبات ریاضی علامت دار برای محاسبه پاسخ در ۴ کلاک خدمتتان ارائه میشود. توجه کنید که به دلیل استفاده از عملگر ضرب به صورت موازی برای محاسبه حاصل ضرب مقادیر علامت دار، باید ملاحظات لازم برای کنترل عرض بیت پاسخ و رشد بیت آن در نظر گرفته شود.
در کد HDL زیر متغیرهای ۱۶ بیتی ورودی با فرمت U1612 به متغیرهای ۱۷ بیتی علامت دار با فرمت Q1712 ارجاع داده شدهاند تا محاسبات به صورت علامت دار انجام شود. علاوه بر این مقادیر ثابت هم با یک بیت اضافه به عنوان بیت علامت ذخیره شدهاند. ذکر این نکته ضروری است که این شیوه پیادهسازی بهترین پیادهسازی ممکن برای این تابع نیست و الگوی به مراتب بهینهتری نیز وجود دارد. اما در اینجا برای بالا بردن کیفیت آموزش و همینطور احترام به حق مالکیت نویسنده اصلی مقاله کدها بدون کم و کاست ارائه شده است.
-- copyright 2019 hexalinx.com
entity transfer_function is port(
Clk : in std_logic;
Rst : in std_logic;
Data_i : in std_logic_vector(15 downto 0);
Valid_i : in std_logic;
result : out std_logic_vector(15 downto 0);
new_res : out std_logic);
end entity transfer_function;
architecture rtl of transfer_function is
-- this module performs the following transfer function -0.0088x2 + 1.7673x + 131.29
-- input Data_i is scaled 8,8, while the output Data_i will be scaled 8,8.
-- this module utilizes signed parallel mathematics
constant c : signed(16 downto 0) := to_signed(-577,17); -- -0.0088*2**16
constant b : signed(16 downto 0) := to_signed(57910,17); -- 1.7673*2**15
constant a : signed(16 downto 0) := to_signed(33610,17); -- -0.0088*2**8
type CONTROL_STATE is (IDLE, MULTIPLY, ADD, RESULT_OP);
signal pre_state : CONTROL_STATE;
signal Valid_in_reg1: std_logic; --used to detect rising edge upon the Valid_i
signal squared : signed(33 downto 0); -- register holds input squared.
signal cx2 : signed(50 downto 0); -- register used to hold cx2
signal bx : signed(33 downto 0); -- register used to hold bx
signal res_int : signed(16 downto 0); -- register holding the temporary result
begin
FSM:
process(Clk)
begin
if rising_edge(Clk) then
if Rst = '1' then
Valid_in_reg1 <= '0';
squared <= (others => '0');
cx2 <= (others => '0');
bx <= (others => '0');
result <= (others => '0');
res_int <= (others => '0');
new_res <= '0';
pre_state <= IDLE;
else
Valid_in_reg1 <= Valid_i;
case pre_state is
when IDLE =>
new_res <= '0';
if (Valid_i = '1') and (Valid_in_reg1 = '0') then -- detect rising edge new Data_i
squared <= signed('0'& Data_i) * signed('0'& Data_i);
pre_state <= MULTIPLY;
else
squared <= (others =>'0');
pre_state <= IDLE;
end if;
when MULTIPLY =>
new_res <= '0';
cx2 <= (squared * c);
bx <= (signed('0'& Data_i)* b);
pre_state <= ADD;
when ADD =>
new_res <= '0';
res_int <= a + cx2(48 downto 32) + ("000"& bx(32 downto 19));
pre_state <= RESULT_OP;
when RESULT_OP =>
result <= std_logic_vector(res_int (res_int'high -1 downto 0));
new_res <= '0';
pre_state <= IDLE;
end case;
end if;
end if;
end process;
end architecture rtl;
جمع بندی
معماری تراشههای قابل پیکرهبندی آنها را تبدیل به یک انتخاب ایدهال برای پیادهسازی توابع ریاضی کرده است. البته باید بخاطر داشته باشیم که پیادهسازی الگوریتمهای ریاضی کمی نیاز به مدل سازی و طراحی سطح بالا در ابزارهایی همچون Matlab دارد. بعد از مسلط شدن به مبانی محاسبات ریاضی در تراشههای قابل پیکرهبندی، پیادهسازی انواع توابع پیچیده ریاضی و الگوریتمهای پردازش سیگنال به سادگی امکانپذیر میشود.
اصول کلی که در این مقاله بیان گردید، کاملا بر پایه مفاهیم بنیادی در پیادهسازیهای ممیز ثابت بنا شده است و در آن از قابلیتهای ابزارهایی نظیر Matlab استفاده نشده است. استفاده از ابزارهای مدرن طراحی فرایند پیادهسازی را به شدت تسریع و تسهیل میکند.
منبع: با اقتباس از Xcell Journal







4 دیدگاه برای “مبانی محاسبات ریاضی در FPGA (قسمت دوم)”
مطالب کمی سنگین بیان شده اما روندش خوبه. با تشکر
سلام بر شما
از اینکه نظر با ارزشتون را با ما در میان گذاشتید، سپاسگزاریم.
در صورت نیاز میتوانید در مورد بخشهای مبهم سوألاتتون را مطرح بفرمایید.
سخت ترین مبحث ریاضی رو از اینجا یاد گرفتم مرررسی
امیدوارم پیروز و سربلند باشید.