کار با حلقه‌ها در HLS

مقدمه

وقتی که شروع به کدنویسی برای پیاده‌سازی‌ یک ماژول در HLS‌ می‌کنیم، احتمالاً هدف ما پیاده‌سازی الگوریتم‌هایی است که وظیفه پردازش بلوک‌های داده را به صورت تکرار شونده برعهده دارند. برای مثال بسیاری از الگوریتم‌های پردازش تصویر و پردازش سیگنال به این شکل هستند. این الگوریتم‌ها تعدادی زیادی عملیات ضرب و جمع دارند و در داخل حلقه‌های متعدد اجرا می‌شوند.

بنابراین، کدهای HLS‌ ما چه از نوع C و چه از نوع ++C احتمالا دارای تعدادی حلقه پشت سرهم و یا حلقه‌های تو در تو هستند. وقتی صحبت از بهینه سازی کدها در HLS به میان می‌آید. بررسی و بازبینی کارایی حلقه‌ها یکی از مواردی است که می‌تواند ما را در دستیابی به نتایج مطلوب یاری برساند. در این آموزش از پایگاه دانش هگزالینکس قصد داریم شما را با روش‌های معمول بهینه سازی و کار حلقه‌ها در HLS آشنا کنیم. دایرکتیوها و پراگماهای مهم را معرفی می‌کنیم و اثر اعمال آن‌ها روی حلقه‌ها را بررسی می‌کنیم. اگر علاقمند به یادگیری این اصول هستید، این مطلب را تا انتها و به دقت مطالعه کنید. با وجود اینکه بخش زیادی از مطالب مهم این آموزش در انتهای کار توضیح داده می‌شود، ولی درک آن‌ها تنها با یادگیری مطالب مقدماتی ابتدایی امکان‌پذیر است.

دستیابی به بهترین کارایی در استفاده از حلقه‌ها

به صورت پیش فرض، حلقه‌ها در HLS به صورت پشت سرهم (rolled) هستند. یعنی هر تکرار حلقه بعد از اتمام اجرای قبلی و دقیقاً با استفاده از منایع سخت افزاری یکسان انجام می‌شود. کاملاً واضح است که با توجه به توالی ذاتی موجود در اجرای محاسبات، زمان مورد نیاز برای اتمام محاسبات به شدت افزایش می‌یابد. به این ترتیب استفاده از حالت پیش فرض HLS بدترین کارایی و کمترین منابع مصرفی را به همراه دارد.

برای شروع بد نیست باهم یک جمع کننده انباره (accumulator)، مشابه شکل زیر در نظر بگیریم.

int accum (int a[3])
{
	int i;
	int b;
	b = 0;
	accum_loop: for(i=0;i<3;i++){
		b = b + a[i];
	}
	return b;
}

در ابتدای کار هیچ گونه عملیات بهینه سازی صورت نپذیرفته است. با بررسی روند اجرای سیستم در برگه analysis view از ابزار Vivado-HLS به سادگی در می‌یابیم که اجرای محاسبات کاملاً ترتیبی و پشت سرهم است. برای حصول اطمینان از این مسأله تنها کافی است به مقدار پارامتر tripcount نگاهی بیاندازیم. پارامتر tripcount تعداد دفعات اجرای حلقه را گزارش می‌کند. در کنار پارامتر tripcount مقدار پارامتر initiation interval نیز قابل مشاهده است. پارمتر initiation interval بیانگر تعداد کلاک‌های مورد نیاز ماژول پیش از پذیرش ورودی‌های جدید است. به بیان دیگر این پارامتر حداقل تعداد کلاک‌هایی را که ماژول HLS باید منتظر بماند و بعد از آن آماده پذیرفتن مقادیر جدید در ورودی بشود، گزارش می‌کند. تأخیر اجرای حلقه برابر با حاصلضرب این دو پارامتر است.

همواره دو اصل کلی برای بهینه سازی در HLS باید مد نظر قرار بگیرد.

• برای دستیابی بهترین توان عملیاتی (throughput)، باید تا حد امکان فاصله زمانی بین ورودی‌های متوالی را کاهش دهیم، یعنی بهینه سازی را با هدف حداقل کردن مقدار پارامتر initiation interval انجام دهیم.
• برای بالابردن کارایی (performance)، باید حلقه‌ها را باز کنیم (unroll) و پیاده‌سازی را به صورت کاملا موازی انجام دهیم. نرخ موازی سازی معمولاً متناسب با تعداد دفعاتی که حلقه اجرا می‌شود، تعیین می‌گردد. توجه شود که آرگومان مشخص کننده تعداد دفعات تکرار حلقه (مثلا متغییر i در کد زیر) باید مقداری ثابت باشد.

int accum (int a[3])
{
	int i;
	int b;
	b = 0;
	#pragma HLS UNROLL
	accum_loop: for(i=0;i<3;i++){
		b = b + a[i];
	}
	return b;
}

بعد از استفاده از پراگمای unroll و بلافاصله بعد از سنتز کدهای HLS مشاهده خواهیم کرد که باز کردن حلقه‌ها در HLS ، یک کاهش قابل ملاحظه در مقدار پارامتر Initiation Interval به همراه دارد. در واقع مقدار آن از ۸ به ۳ کاهش می‌یابد.

در گزارش سنتز با توجه به اینکه حلقه کاملا باز شده‌ است (unrolled) و در عمل دیگر حلقه‌ای وجود ندارد، مقداری برای پارامتر tripcount نمایش داده نمی‌شود.

باز کردن حلقه‌ها در کنار افزایش چشمگیر کارایی جمع کننده، باعث بالا رفتن منابع مصرفی روی تراشه نیز می‌شود. از این رو باید یک مصالحه برای اعمال مناسب بهینه سازی روی طرح در نظرگرفته شود. موارد فراوانی وجود دارد که در آن نه زمان اجرای محاسبات در حالت rolled و نه منابع مصرفی طرح در حالت unrolled برای ما مطلوب نیست. در صورتی که بعد از باز کردن حلقه‌ها امکان پذیرش سربار و منابع مصرفی اضافی ناشی از آن برای ما مقدور نباشد، ناچاریم از بازکردن کامل حلقه‌ها پرهیز کنیم و تنها بخشی از تکرارهای حلقه‌ها را به صورت موازی پیاده‌سازی کنیم. به نوعی یک پیاده‌سازی ترکیبی سریال و موازی انجام دهیم. برای درک بهتر این نکته اجازه بدهید سایز جمع کننده‌ای را که طراحی کردیم، تغییر بدهیم و نتیجه را مجدد با هم بررسی کنیم. این با سایز جمع کننده انباره را از ۳ به ۵۰ افزایش می‌دهیم.

باز کردن حلقه‌ها در کنار افزایش چشمگیر کارایی جمع کننده، باعث بالا رفتن منابع مصرفی روی تراشه نیز می‌شود. از این رو باید یک مصالحه برای اعمال مناسب بهینه سازی روی طرح در نظرگرفته شود.

با تغییر مقدار factor در پراگمای unroll می‌توانیم میزان موازی سازی حلقه را کنترل کنیم. (به کدهای زیر دقت کنید).

int accum (int a[50])
{
	int i;
	int b;
	b = 0;
	accum_loop: for(i=0;i<50;i++){
	#pragma HLS UNROLL factor 2
		b = b + a[i];
	}
	return b;
}

برگه performance profile گزارش نهایی پیاده‌سازی کارایی جمع کننده را با توجه به فاکتور مورد استفاده برای موازی سازی، گزارش می‌کند. در این مثال، تأخیر پیاده‌سازی نسبت به حالت پیش فرض اولیه (rolled)، به نصف کاهش پیدا کرده است.

در صفحه schedule viewer این مسأله به صورت گرافیکی قابل مشاهده است. در این صفحه جزئیات بیشتری از نحوه پیاده‌سازی الگوریتم نیز در دسترس طراح قرار داده شده است.

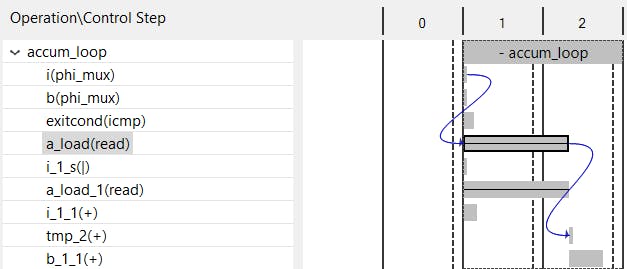
وقتی تنها بخشی از کد یا به عبارت دقیق تر بخشی از یک حلقه unroll می‌شود، ابزار Vivado-HLS شرط خروج از حلقه را در حالتی که مقدار انتخابی برای فاکتور منجربه به موازی سازی با یک مقدار صحیح نشود، بررسی می‌کند. با این وجود اگر مقدار آن صحیح باشد، ما می‌توانیم از بررسی این شرط صرف نظر کنیم.

حالا سوال اینجاست، در صورتی که حلقه‌ها به صورت تو در تو باشند، روند اجرای آن‌ها چگونه مدیریت می‌شود؟ شرایطی را در نظر بگیرید که در آن نیازمند انجام محاسباتی ماتریسی یا پردازش تصویر هستیم.

در چنین شرایطی، چندین انتخاب وجود دارد که کاملا وابسته به نحوه پیاده‌سازی حلقه است. به منظور دستیابی به حداکثر کارایی (یعنی کمترین تأخیر)، در زمان کار با حلقه‌های تو در تو، ما باید ابتدا حلقه‌های تو در توی کامل ایجاد کنیم (perfect nested loop).

حلقه‌های تو در توی کامل دارای دو ویژگی هستند:

• همچون قبل آرگومان تکرار حلقه‌ها مقدرای ثابت است.
• و کلیه محاسبات داخل بدنه درونی ترین حلقه اجرا می‌شوند.

// perfect loop
perfect_loop_1: for( x = 0; x < n; x++) {
	perfect_loop_2: for( y = 0; y < m; y++) {
	
	// perfect loop code inserted here
	}
}

// imperfect loop
imperfect_loop_1: for( x = 0; x < n; x++) {
	// imperfect loop contain code here
	imperfect_loop_2: for( y = 0; y < m; y++) {
	
	// imperfect loop code inserted here
	}
}

در صورتی که حلقه‌ها کامل باشند، امکان یکپارچه کردن (flatten) حلقه‌های تو در تو و ترکیب (merge) حلقه‌های پشت سرهم با استفاده از دایرکتیوهای loop_flatten و loop_merge در HLS وجود دارد. این کار باعث بهبود نتایج پیاده‌سازی بعد از سنتز می‌شود.

مقدار پارامتر tripcount یک حلقه بعد از یکپارچه شدن برابر با حاصلضرب m×n است. دو عدد m و n به ترتیب تعداد تکرارهای حلقه‌های داخلی و خارجی هستند.

از سوی دیگر در صورتی که در کد ما چندین حلقه پشت سرهم وجود داشته باشد، که به صورت پیاپی فراخوانی و اجرا می‌شوند، می‌توان با استفاده از دایرکتیو loop_merge آن ها را با هم ترکیب کرد.

نکته حائز اهمیت در اینجا تفاوت دو دایرکتیو یکپارچه سازی (loop_flatten) و ترکیب (loop_merge) است. در HLS با دایرکتیو پکپارچه سازی عملاً دو یا چند حلقه تو در تو با هم درون یک حلقه تجمیع می‌شوند، در حالی که با دایرکتیو ترکیب دو یا چند حلقه مستقل و پشت سرهم در یک حلقه تجمیع می‌شوند.

loop_1: for( x = 0; x < n; x++) {
    // loop one content
}
loop_2: for( y = 0; y < m; y++) {
    // loop two content
}
loop_3: for( i = 0; i < p; i++) {
    // loop three content
}

ترکیب حلقه‌ها در HLS از تأخیر تجمیعی سیستم می‌کاهد و روند به اشتراک گذاری منابع منطقی را بهبود می‌بخشد، چون کلاک‌های اضافی مورد نیاز برای گذر بین بدنه حلقه‌ها در زمان پیاده‌سازی کاهش می‌یابد.

در صورتی که تصمیم به ترکیب چند حلقه دارید، بهتر است کمی صبر کنید و قبل از شروع به کار، چند محدودیت مهم را در نظر بگیرید.

• ما قادر به ترکیب حلقه‌هایی که ورودی خروجی آن‌ها به صورت FIFO تعریف شده است، نیستیم.
• در صورت متغیر بودن مقدار آرگومان تکرار حلقه‌ها امکان ترکیب آن‌ها وجود ندارد.
• کدهای بین حلقه‌ها نباید داری اثر جانبی (side effect) باشند یعنی مجاز به استفاده از عملیاتی مثل a=a+1 بین دو حلقه نیستیم، چون با هر بار تکرار مقدار آن تغییر می‌کند.

مرور مطالب تئوری کافیست، اجازه بدهید برای درک بهتر موضوع با هم مثالی را از نحوه ترکیب حلقه‌ها مرور کنیم. فرض کنیم کدهای HLS به صورت زیر است.

int accum (int a[50])
{
	int x,y,i;
	int b[5];
	int c[5];
	int d;

	loop_1: for( x = 0; x < 50; x++) {
		// loop one content
		b[x] = a[x] + 100;
	}
	loop_2: for( y = 0; y < 50; y++) {
		// loop two content
		c[y] = b[y] * 2;
	}
	loop_3: for( i = 0; i < 50; i++) {
		// loop three content
		d = d + c[i];
	}
}

با سنتز این کدها به صورت پیش فرض، یعنی بدون استفاده از دایرکتیوها، پارامترهای latency و پراگمای HLS loop merge به صورت زیر خواهد بود.

با ترکیب حلقه احتمالا نتایج سنتز تغییر می‌کند، پس از دایرکتیو loop_merge به شکل یک پراگما درون کد به صورت زیر استفاده می‌کنیم.

int accum (int a[50])
{
	int x,y,i;
	int b[5];
	int c[5];
	int d;

	loop_1: for( x = 0; x < 50; x++) {
	#pragma HLS LOOP_MERGE
		// loop one content
		b[x] = a[x] + 100;
	}
	loop_2: for( y = 0; y < 50; y++) {
	#pragma HLS LOOP_MERGE
		// loop two content
		c[y] = b[y] * 2;
	}
	loop_3: for( i = 0; i < 50; i++) {
	#pragma HLS LOOP_MERGE
		// loop three content
		d = d + c[i];
	}
}

با ترکیب حلقه به وضوح کاهش تاحیر تجمیعی نتایج را می‌توان مشاهده نمود. نتایج آن برگه performance profile قابل مشاهده است.

جمع بندی

وقتی صحبت از بهینه سازی کدهای HLS‌ به میان می‌آید، موارد و جنبه‌های زیادی برای بهینه سازی وجود دارد. تنها با باز کردن و یا ترکیب حلقه‌ها ممکن است به نتایج مطلوب نرسیم. پاپلاین کردن محاسبات، پایپلاین کردن نحوه خواندن و نوشتن داده‌ها درون حافظه و چندین و چند مفهوم دیگر برای رسیدن به بهینه ترین پاسخ باید مد نظر قرار داده شود. در این مقاله نحوه کار با حلقه‌ها در HLS را با هم مرور کردیم، منتظر مقالات آموزشی بعدی باشید.

منبع: با اقتباس از hackster.io  نوشته Adam Taylor