محاسبه سینوس و کسینوس در FPGA با استفاده از CORDIC

مقدمه

در این مقاله از سری آموزش‌های پایگاه دانش هگزالینکس باهم مروری بر چگونگی تجمیع یکی از پرکاربردترین IP Core های Xilinx در یک طراحی FPGA خواهیم داشت. ما قصد داریم از CORDIC IP Core برای محاسبه مقدار سینوس و کسینوس یک زاویه دلخواه استفاده کنیم. در طول این آموزش بعد از یک معرفی کوتاه از الگوریتم CORDIC و جایگاه آن در پیاده سازی توابع ریاضی پایه، فرایند سفارشی سازی و فراخوانی این IP Core‌ را مرور خواهیم کرد. همچنین مشخصه‌ها و خصوصیات CORDIC IP Core را موشکافانه بررسی خواهیم کرد. اگر علاقمند به فراگیری یکی از راه‌های محاسبه سینوس و کسینوس در FPGA هستید، تا انتها با ما همراه شوید.

معرفی الگوریتم CORDIC

واژه CORDIC مخفف عبارت COordinate Rotation DIgital Computer است و از نقطه نظر پیاده سازی یک الگوریتم کاملاً بهینه یا اصطلاحاً Hardware-efficient است که با استفاده از یک متد تکرار شونده مبتنی بر چرخش و دَوَران ، برای پیاده سازی سخت افزاری رنج وسیعی از توابع پایه‌ای ریاضی بکار برده می‌شود.

مهمترین نکته‌ای که در همین ابتدا ممکن است نظر شما را به خودش جلب کند کلید واژه‌های چرخش و دَوَران است. برای چند لحظه همه چیز در رابطه با الکترونیک و FPGA را فراموش کنید و به گذشته برگردید، منظورم زمانی است که در دبیرستان مشغول تحصیل بودید. با کمی تمرکز حتماً می‌توانید تعدادی از محاسبات ریاضی را که تنها با چرخاندن یک بردار قابل انجام بودند، بخاطر بیاورید. منظور من از بردار، برداری است که از مبدأ مختصات شروع می‌شود و به یک نقطه روی دایره مثلثاتی ختم می‌شود.

فرض کنید که یک سیستم کاملاً ایده‌ال داریم که یک بردار را دریافت می‌کند و آن را به اندازه زاویه انتخابی (Ѳ) دَوَران می‌دهد. اگر نقطه اولیه (x_in,y_in) باشد، نقطه جدید (x_R,y_R) خواهد بود. زاویه بین بردارهایی که این دو نقطه را به هم متصل می‌کنند برابر (Ѳ) خواهد بود. شکل زیر گویای همه چیز است.

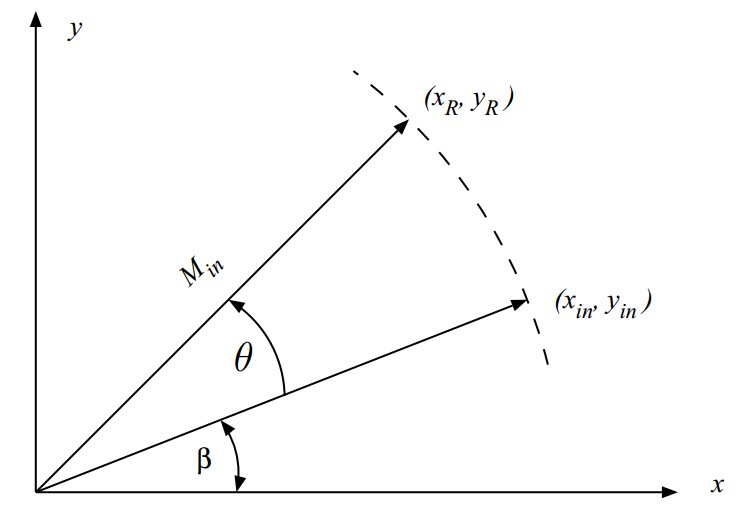
با استفاده از توابع مثلثاتی مختصات نقطه جدید را می‌توان برحسب نقطه اولیه بیان کرد است. کافی است از روابط زیر استفاده کنیم.

\[x_R = x_{in} cos(\theta) – y_{in} sin(\theta)\]

\[y_R = x_{in} sin(\theta) + y_{in} cos(\theta)\]

اگر فرض کنیم که مختصات نقطه اولیه x_in=1  و y_in=0 است. بعد از چرخش به اندازه زاویه (Ѳ) نقطه حاصل برابر خواهد بود با:

\[x_R = cos(\theta)\]

\[y_R = sin(\theta)\]

خب جالب شد. حالا اگه قصد ما حساب کردن سینوس و کسینوس زاویه (Ѳ) باشد، خیلی ساده با استفاده از روابط فوق به پاسخ خودمان رسیدیم. یعنی یک نقطه را روی صفحه مختصات به اندازه زاویه مد نظرمان چرخاندیم و به راحتی سینوس و کسینوس زاویه مورد نظر را بدست آوردیم.

اجازه بدهید یک مثال دیگر را هم بررسی کنیم و ببینیم چه چیزهای دیگری را می‌توانیم با با دوران دادن نقاط حساب کنیم. نظر شما در رابطه با محاسبه اندازه یک بردار چیست؟ همانطور که می‌دانید اندازه یک بردار با استفاده از رابطه زیر محاسبه می‌شود.

\[\sqrt{x_{in}^2 + y_{in}^2}\]

برای محاسبه اندازه هم ما فقط نیاز داریم بردار ورودی را کمی بچرخانیم. به شکلی که دقیقاً با محور افقی تراز بشود. یعنی بردار ما کاملاً بر روی محور افقی منطبق شود. در این حالت مقدار y_in=0 خواهد بود و اندازه بردار برابر با x_in خواهد بود. یکی از سوألاتی که ممکن است در همین لحظه به ذهن شما رسیده باشد، این است که برای منطبق کردن بردار روی محور افقی نقاط (x_in,y_in) را باید حدوداً چند درجه بچرخانیم؟ و یا اینکه اصلاً چگونه این دوران را انجام بدهیم؟ لطفاً کمی صبر داشته باشید، در این رابطه بیشتر صحبت خواهیم کرد.

قبل از اینکه وارد روابط ریاضی بشویم دوست دارم اشاره‌ای به توابعی که به این صورت قابل محاسبه هستند، داشته باشم، تعداد این توابع نسبتاً قابل توجه هست. بهترین مثال‌هایی که می‌توان ارائه کرد، توابع معکوس مثلثاتی مثل arctan و arcsin و یا arccos است. توابع هایپربولیک و لگاریتمی هم گزینه‌های مناسبی برای پیاده سازی با الگوریتم CORDIC هستند. همینطور توابع مورد استفاده برای تبدیل‌ نقاط در دستگاه‌های مختصات (از کارتزین به قطبی و برعکس) از دیگر توابع مهمی هستند که می‌‌توان از آن ها نام برد.

الگوریتم کوردیک (CORDIC) تلاش می‌کند که یک روش کاملاً بهینه و اصطلاحاً Hardware-efficient برای محاسبه این توابع ارائه بدهد. عبارت Hardware-efficient به این معناست که در پیاده سازی این الگوریتم تنها از دو عملگر جمع و تفریق به همراه شیفت استفاده می‌شود و هیچ بلوک ضرب کننده‌ایی در آن استفاده نمی‌شود. دقت کنید که در سایر متدها، پیاده سازی چنین توابعی (مثلاً متد استفاده از سری‌های توانی برای محاسبه توایع مثلثاتی) در نهایت نیاز به ضرب کننده دارند و این برگ برنده الگوریتم CORDIC در مقابل سایر الگوریتم‌ هاست.

ما قصد نداریم خیلی موضوعات تئوریک الگوریتم کوردیک (CORDIC) را توضیح بدهیم. اما برای اینکه حس خوبی نسبت به اصول کار آن داشته باشید، کمی و فقط کمی از مبانی آن را با هم مرور می‌کنیم.

مبانی الگوریتم CORDIC

در ابتدای کار رابطه‌ایی را که در شروع این مقاله دیدیم، به شکل زیر بازنویسی می‌کنیم.

\[\begin{bmatrix} x_{R} \\ y_{R} \end{bmatrix} = cos(\theta) \begin{bmatrix} 1 & -tan(\theta) \\ tan(\theta) & 1 \end{bmatrix} \begin{bmatrix} x_{in} \\ y_{in} \end{bmatrix}\]

رابطه بالا به ما نشان می‌دهد که برای اجرای یک چرخش نیاز به انجام چهار عمل ضرب به علاوه چند عمل جمع و تفریق داریم. قبلاً اشاره کردیم که این الگوریتم Hardware-efficient است، حالا سوأل اینجاست که چگونه از انجام این ضرب‌ها اجتناب کنیم؟ الگوریتم CORDIC برای انجام یک دوران بدون استفاده از حتی یک ضرب کننده از دو ایده بنیادی پیروی می‌کند.

ایده بنیادی اول این است که دوران یک بردار با یک زاویه دلخواه (Ѳ_d) برابر با چرخاندن همان بردار با تعداد زیادی زوایه کوچکتر است بطوریکه مجموع این زوایای کوچکتر برابر با زاویه اولیه باشد. به این صورت:

\[theta_{d} = \sum_{i=0}^{n} \theta_{i}\]

مثلا زاویه 57.535˚ برابر با حاصل جمع زوایای ˚45 و ˚25.565 و ˚14.3- درجه است. دقت کنید که ما زاویه منفی هم داریم، این یعنی چرخش در جهت عقربه‌های ساعت نیز مجاز است.

ایده بنیادی دوم به این شکل است که ما می‌توانیم زوایای انتخابی را به اندازه‌ایی کوچک انتخاب کنیم که در آن رابطه زیر برقرار باشد:

\[tan(\theta_{i}) = 2^{-i}\]

به این ترتیب ضرب در عبارت (tan(Ѳ می‌تواند نتها با چند بیت شیف جایگزین شود که یک مزیت بسیار بزرگ است. حالا ممکن است از خودتان بپرسید با توجه به زوایه (Ѳ_d) چگونه می‌توانیم همزمان این دو ایده را اجرا کنیم، یعنی:

\[\theta_{d} = \sum_{i=0}^{n} \theta_{i} \:\: while \:\:\: tan(\theta_{i}) = 2^{-i}\]

نکته‌ای که باید به آن توجه کنیم این است که، در حالت کلی نتیجه نهایی دقتی محدود دارد و پاسخ‌ها کاملاً دقیق نخواهد بود چون زاویه نهایی ممکن است با زاویه مطلوب کمی متفاوت باشد. پارامتر n یعنی تعداد دفعات تکرار رابطه مستقیم با دقت پاسخ دارد، از این رو هر چقدر n بزرگتر باشد تعداد زوایا و به عبارتی تعداد دفعات تکرار الگوریتم افزایش می‌یابد و در نتیجه پاسخ دقیق تر می‌شود.

اما کار هنوز تموم نشده است، اگر چه جایگزینی عبارت (tan(Ѳ با توان‌های منفی دو باعث حذف دو عملیات ضرب شد ولی دو عملیات ضرب دیگر در عبارت (cos(Ѳ باقی مانده است. ما می‌توانیم ضریب (cos(Ѳ را گین سیستم در نظر بگیریم، چون هم در x و هم در y ضرب می‌شود. یک ایده مناسب برای اجتناب از ضرب این گین، فاکتورگیری از آن در ابتدای کار و بازگرداندن آن در انتهای محاسبات است. از این رو به ضریب (cos(Ѳ فاکتور مقیاس بندی یا scaling factor هم می‌گویند. ما اگر در هنگام دوران زوایا این فاکتور را حذف کنیم بازهم زاویه پایانی صحیح خواهد بود با این تفاوت که ما نیاز داریم در انتهای کار ضریب حذف شده را مجددأ روی خروجی اعمال کنیم و (x_R,y_R) را بدست بیاوریم زیرا در صورت حذف فاکتور مقیاس بندی به جای (x_R,y_R) به (x’_R,y’_R) می‌رسیم. در واقع ما با حذف فاکتور (cos(Ѳ از پاسخ، پاسخی بدست آورده‌ایم که به اندازه ^1-(cos(Ѳ برابر بزرگتر از پاسخ اصلی (x_R,y_R) است. این مسأله در شکل زیر نشان داده شده است.

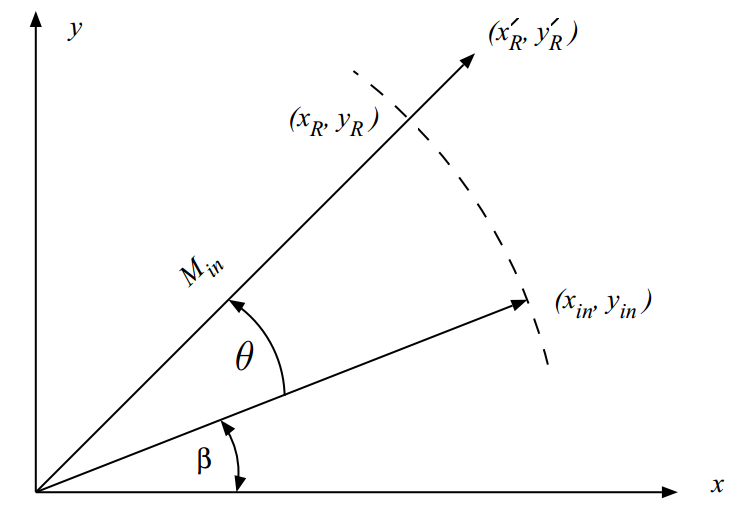
حالا بد نیست برای اینکه درک بهتری از روند اجرای الگوریتم داشته باشیم یک مثال عددی را با هم مرور کنیم.

مثال عددی

فرض کنید قصد داریم بردار ورودی را با زاویه ˚57.535 دوران دهیم. بنابر این نیاز داریم دوران‌های زیر را به ترتیب روی بردار ورودی اعمال کنیم.

45˚ + 25.565˚- 14.3˚

اولین دوران با زاویه ˚45 بصورت زیر انجام می‌شود:

$$\begin{bmatrix} x_{0} \\ y_{0} \end{bmatrix} = cos(45˚) \begin{bmatrix} 1 & -1 \\ 1 & 1 \end{bmatrix} \begin{bmatrix} x_{in} \\ y_{in} \end{bmatrix} $$

دومین دوران نیز به شکل زیر خواهد بود:

$$\begin{bmatrix} x_{1} \\ y_{1} \end{bmatrix} = cos(26.565˚) \begin{bmatrix} 1 & -2^{-1} \\ 2^{-1} & 1 \end{bmatrix} \begin{bmatrix} x_{0} \\ y_{0} \end{bmatrix}$$

با ادغام روابط فوق و کمی ساده سازی خواهیم داشت:

$$\begin{bmatrix} x_{1} \\ y_{1} \end{bmatrix} = cos(45˚) cos(26.565˚) \begin{bmatrix} 1 & -1 \\ 1 & 1 \end{bmatrix} \begin{bmatrix} 1 & -2^{-1} \\ 2^{-1} & 1 \end{bmatrix} \begin{bmatrix} x_{in} \\ y_{in} \end{bmatrix}$$

سومین دوران هم به صورت زیر خواهد بود:

$$\begin{bmatrix} x_{2} \\ y_{2} \end{bmatrix} = cos(-14.03˚) \begin{bmatrix} 1 & 2^{-2} \\ -2^{-2} & 1 \end{bmatrix} \begin{bmatrix} x_{1} \\ y_{1} \end{bmatrix}$$

و در نهایت پاسخ برابر خواهد بود با:

$$\begin{bmatrix} x_{2} \\ y_{2} \end{bmatrix} = cos(45˚) cos(26.565˚) cos(-14.03˚) \begin{bmatrix} 1 & -1 \\ 1 & 1 \end{bmatrix} \begin{bmatrix} 1 & -2^{-1} \\ 2^{-1} & 1 \end{bmatrix} \begin{bmatrix} 1 & 2^{-2} \\ -2^{-2} & 1 \end{bmatrix} \begin{bmatrix} x_{in} \\ y_{in} \end{bmatrix}$$

در رابطه بالا نیاز است که به دو نکته توجه کنید. اول اینکه هر دوران یک فاکتور مقیاس بندی مستقل دارد که می‌تواند در گام‌های تکرار الگوریتم کنار گذاشته شود و در انتها لحاظ شود و دوم اینکه زاویه دوران با هر بار تکرار کوچکتر می‌شود.

با کمی محاسبه به سادگی می‌توان اثبات کرد با کوچکتر شدن زاویه در صورتی که حداقل ۶ تکرار از الگوریتم اجرا شود مقدار فاکتور مقیاس بندی به سمت یک عدد مشخص میل می‌کند. این عدد را K می‌نامیم و برابر است با K=0.6072.

$$K \approx cos(45˚) cos(26.565˚) \times \dots \times cos(0.895˚) = 0.6072$$

پس با توجه به توضیحات فوق می‌توانیم از همه فاکتورهای مقیاس بندی در طول محاسبات صرف نظر کنیم و در نهایت فارغ از اینکه زاویه دوران چند درجه است، مقیاس پاسخ نهایی را با عدد K اصطلاح کنیم. احتمالاً الان دارید فکر می‌کنید که باز هم در انتهای کار یک ضرب خواهیم داشت، اما اینطور نیست! این فاکتور معمولاً به عنوان یک مقدار اولیه در سیستم ذخیره می‌شود و هیچگاه ضربی انجام نمی‌شود.

مباحث تئوریک تا همینجا کافیه، هدف ما این بود که کمی با ایده اصلی پشت این الگوریتم آشنا بشوید. بهتره کار را شروع کنیم و روی پیاده سازی توابع سینوس و کسینوس با اگوریتم CORDIC تمرکز کنیم.

پیاده سازی توابع سینوس و کسینوس

پیاده سازی و شبیه سازی با استفاده از نسخه 14.7 مجموعه نرم افزاری ISE صورت پذیرفته است. با فرض اینکه شما آشنایی کافی با شیوه ساخت پروژه در ISE Project Navigator دارید، مستقیمأ به سراغ فراخوانی CORDIC IP Core‌ می‌رویم. برای اضافه کردن IP Core به پروژه ISE به صورت زیر عمل کنید.

۱- در منوی Project روی گزینه New Source کلیک کنید و از لیست موجود گزینه IP (CORE Generator & Architecture Wizard) را مطابق با آنچه در شکل زیر نشان داده شده است، انتخاب کنید.

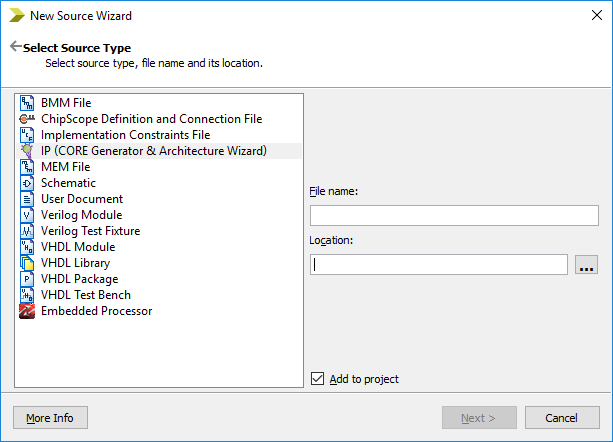
۲- برای فایل خود یک نام انتخاب کنید و آدرس مورد نظر برای ذخیره سازی را تعیین کنید. روی Next کلیک کنید. در صفحه بعدی ویزارد لیست تمامی IP Core‌ های موجود و قابل فراخوانی در ISE را خواهید دید.

۳- از لیست موجود با تایپ عبارت CORDIC‌ در فیلد Search IP Catalog گزینه CORDIC 4.0 را انتخاب کنید.

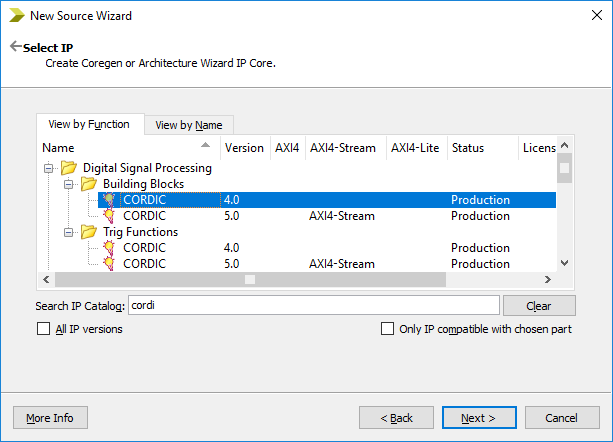
۴- در انتها صفحه Summary ظاهر می‌شود، روی Finish کلیک کنید تا IP Core به پروژه اضافه شود.

در ادامه ویزارد تنظیمات IP به صورت اتوماتیک روی صفحه ظاهر می‌‌شود. در این صفحه با توجه به نیاز خودتان تنظیمات IP را سفارشی سازی کنید.

تنظیم پارامترهای IP Core

ویزارد تنظیمات این IP متشکل از سه صفحه است که تنظیمات موجود در اولین صفحه آن نیز در سه بخش دسته بندی شده است. در سمت چپ این صفحه می‌توانید شماتیک و ورودی/خروجی‌های فعال آن را تب IP Symbol مشاهده کنید. این ورودی/خروجی‌ها با توجه به انتخاب‌های شما تغییر خواهند کرد.

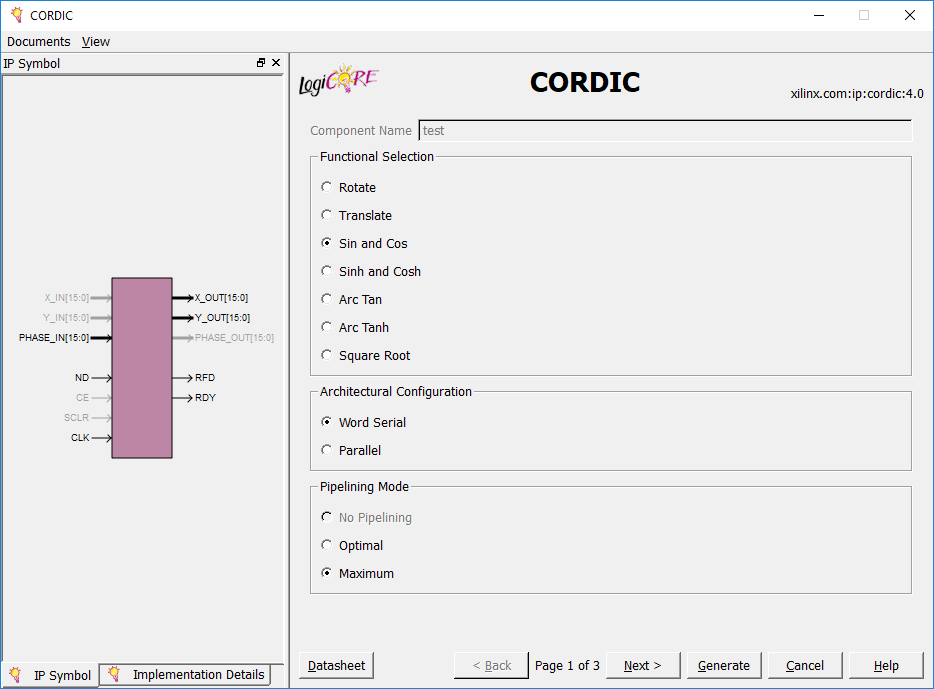
با کلیک روی کلید Datasheet در پایین صفحه شما می‌توانید به سند راهنمای کاربری این IP در سایت Xilinx دسترسی پیدا کنید. در این سند کلیه جزئیات در رابطه با شیوه سفارشی سازی و استفاده از CORDIC IP Core توضیح داده شده است. همینطور به شکل خلاصه تئوری کاری الگوریتم نیز در آن گنجانده شده است. در ادامه ما مهمترین ویژگی‌ها و مشخصه‌های این IP را تشریح خواهیم کرد.

بخش Functional Selection ، به شما اجازه انتخاب فانکشنالیتی مورد نظر را می‌دهد. (می‌توانید فانکشنی را که قصد پیاده سازی آن را دارید، انتخاب کنید). پیش تر اشاره شد که فانکشن‌های متعددی را می‌توان با استفاده از الگوریتم CORDIC پیاده سازی کرد. همانطور که در ابتدا نیز گفتیم ما قصد پیاده سازی توابع مثلثاتی سینوس و کسینوس را داریم. بنابراین گزینه Sin and Cos را انتخاب کنید.

در بخش Architectural Configuration می‌توانید معماری مورد نظر برای پیاده سازی الگوریتم CORDIC را انتخاب کنید. معماری Word Serial با استفاده پیاپی از یک طبقه شیفت و جمع/تفریق، تکرارهای مورد نیاز برای الگوریتم را پیاده سازی می‌کند. به همین دلیل نسبت به سایر معماری‌ها منابع کمتری مصرف می‌کند. اگر چه با اعمال ورودی‌ها ما نیاز خواهیم داشت تا برای چند سیکل کلاک منتظر بمانیم تا خروجی آماده شود.

بخش Pipelining Mode به ما امکان پیاده سازی پایپلاین الگوریتم را می‌دهد. بعضی انتخاب‌ها در این مد پاپلاین ممکن است با توجه به فانکشن و معماری انتخابی غیرفعال باشند. برای مثال در شکل زیر پارامتر No Pipelining غیر فعال است. در این بخش مقادیر پیش فرض را می‌پذیریم و مقدار Maximum را انتخاب می‌کنیم.

با کلیک روی گزینه Next در پایین صفحه به صفحه دوم ویزاد منتقل می‌شوید. تنظیماتی که در این صفحه قرار دارند غالباً به نحوه سفارشی سازی دیتای ورودی می‌پردازند.

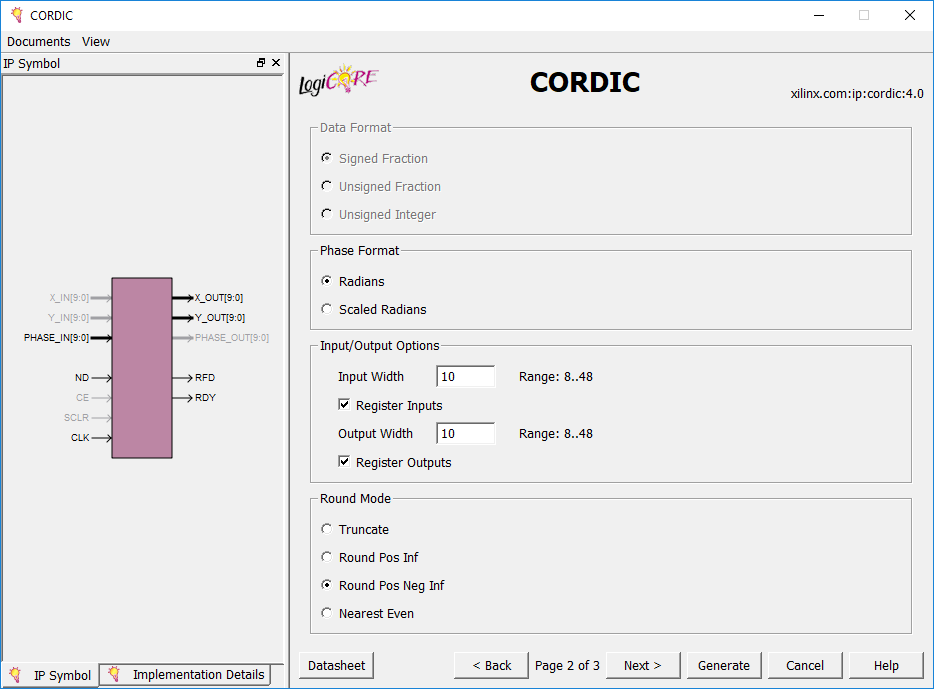
وقتی که برای پیاده سازی سینوس و کسینوس از الگوریتم CORDIC استفاده می‌کنیم، یک ورودی فاز با نام PHASE_IN که همان زاویه است داریم. همینطور دو خروجی X_OUT و YOUT ‌که به ترتیب سینوس و کسینوس زاویه ورودی را خروجی می‌کنند. این ورودی و خروجی با یک نگاه کوتاه به دیاگرام IP Core در سمت چپ به سادگی قابل تشخیص هستند. در صفحه دوم ویزارد شیوه نمایش دیتا روی پورت‌های ورودی و خروجی قابل تنظیم است.

در بخش Data Format نحوه نمایش ورودی‌ها و یا خروجی‌های X و Y تعیین می‌شود. در این پروژه تعیین فرمت خروجی‌های X_OUT‌ و Y_OUT مد نظر ماست.

همانطور که در شکل بالا می‌بینید با توجه به تنظیماتی که تا به اینجا روی IP اعمال کردیم، فرمت به صورت اتوماتیک روی گزینه Signed Fraction تنظیم شده است و امکان ویرایش آن وجود ندارد. با توجه به اطلاعات ارائه شده در دیتاشیت IP ، این دو عدد به صورت ممیز ثابت علامت دار و مکمل دو نمایش داده می‌شوند. عرض (طول) بیت بخش صحیح این اعداد ۲ خواهد بود. چرا؟ دقت کنید که تعداد کل بیت‌های قابل استفاده برای نمایش در فیلد Output Width  قابل سفارشی سازی است اما تعداد بیت‌های صحیح آن همواره برابر با ۲ است. در مثالی که ما برای شما انتخاب کردیم این تعداد ۱۰ در نظر گرفته شده است. بنابراین اگر دیتای خروجی برابر با "0010110101" باشد ما می‌دانیم که نقطه باینری بین بیت شماره ۸ و ۹ است. بنابراین داریم:

00.101101012=0.7070312510

ار آنجایی که داده‌های خروجی علامت دار هستند، بیت سمت چپ بیت علامت است.

بخش بعدی این صفحه به تعیین فرمت ورودی/خروجی فاز اختصاص دارد. برای مد Sin & Cos ما یک ورودی فاز با نام PHASE_IN داریم. با انتخاب گزینه Radians ورودی PHASE_IN به صورت ممیز ثابت مکمل دو در نظر گرفته می‌شود که طول بیت بخش صحیح آن برابر سه بیت است. مجدداً دقت کنید که اینبار تعداد کل بیت‌های ورودی با استفاده از فیلد Input Width  قابل سفارشی سازی است. با توجه به توضیحاتی که ارائه شد، اگر مقدار ورودی PHASE_IN برابر با “0000101011” باشد آنگاه زاویه ورودی برابر با 000.01010112=0.335937510 رادیان خواهد بود. همانطور که در شکل قبلی نشان داده شده است ما از این IP‌ با ورودی و خروجی‌های رجیستر شده استفاده می‌کنیم.

در ادامه در بخش Rounding Mode ، گزینه Round Pos Neg Infinity را انتخاب خواهیم کرد که دقیقاً مشابه فانکشن (Round(x در Matlab‌ است. شما می‌توانید مثال‌‌های متفاوتی را که از سایر مدهای رندینگ که در دیتاشیت توضیح داده شده است، مطالعه کنید.

صفحه سوم تنظیمات در شکل زیر نشان داده شده است.

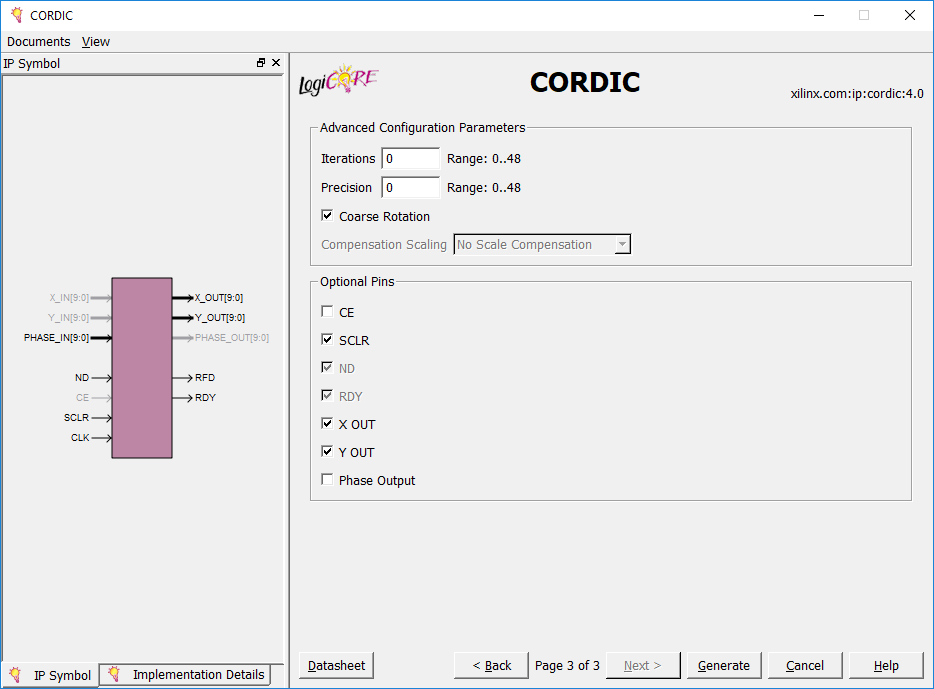
در این صفحه، ما می‌توانیم تعداد تکرار‌های الگوریتم CORDIC و دقت داخلی آن را برای انجام عملیات جمع و تفریق انتخاب کنیم. با توجه به اطلاعات ارائه شده در دیتاشیت، برابر با صفر قرار دادن این دو مقدار نرم افزار را مجبور می‌کند تا به صورت اتوماتیک و با توجه به دقت مورد نیاز خروجی و همینطور سایر پارامترهایی که تا به اینجا تنظیم کردیم، مقدار بهینه را برای آن‌ها تعیین کند. مقدار پیش فرض این دو پارامتر را می‌پذیریم. دقت کنید که تیک گزینه Course Rotation نیز فعال باشد تا تمامی دایره مثلثاتی قابل استفاده باشد.

در آخرین بخش تنظیمات یعنی بخش Optional Pins در این صفحه هم پین‌های ‌کنترلی اختیاری IP Core را تعیین می‌کنیم. ما پورت ورودی سنکرون ریست SCLR را فعال می‌کنیم. وقتی مقدار ‘1’ روی پورت قرار داده شود تمامی رجیسترهای داخلی این IP سنکرون با لبه کلاک مقدار دهی می‌شوند (احتمالاً صفر می‌شوند).

با کلیک روی گزینه Generate‌ در پایین صفحه یک فایل xco تولید می‌شود و یک CORDIC IP Core خروجی به طرح ما اضافه می‌شود. با کلیک و انتخاب گزینه View HDL Instantiation Template در ISE شما قادر به مشاهده الگوی فراخوانی این ماژول درون کدهای اصلی خودتان خواهید بود. با کپی کردن و اضافه کردن این قطعه کد به کدهای اصلی خودتان یک کامپوننت آماده مشابه آنچه احتمالاً تا پیش از این نیز انجام می‌دادید، خواهید داشت. اگر هنوز کدی ندارید کافی است یک تاپ ماژول ساده بنویسید و این IP Core را در آن فراخوانی کنید.

شبیه سازی ISE

برای استفاده از IP Core شما نیاز به مطالعه دقیق بخش Control Signal and Timing در دیتاشیت خواهید داشت. در شکل زیر نحوه استفاده از سیگنال‌های کنترلی برای بکارگیری ساختار Word Serial در IP Core نشان داده شده است.

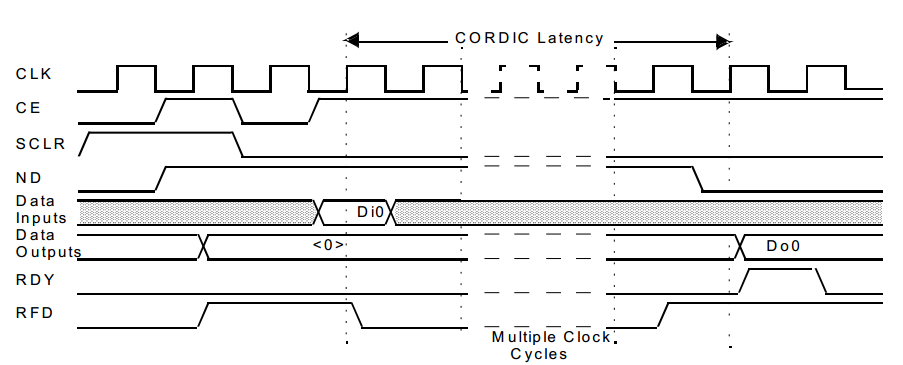
در ابتدا ورودی ریست سنکرون SCLR فعال می‌شود و تمام رجیسترهای داخلی IP Core مقدار دهی می‌شوند. بعد با فعال شدن سیگنال ND به IP اطلاع داده می‌شود که یک داده جدید روی پورت ورودی قرار گرفته است، بنابراین نمونه داده ورودی در لبه بالارونده بعدی کلاک به شرط غیر فعال بودن سیگنال SCLR درون IP نمونه برداری می‌شود.

بعد از به پایان رسیدن محاسبات، IP Core سیگنال خروجی RDY را به نشانه آماده و معتبر بودن داده قرار گرفته روی پورت خروجی فعال می‌کند و همینطور سیگنال خروجی RFD مخفف Ready for Data نیز فعال می‌شود تا آمادگی ماژول برای دریافت و پردازش داده جدید روی پورت ورودی را اعلام کند.

نمونه برداری از نمونه‌های ورودی در اولین لبه کلاک که در آن به صورت همزمان دو سیگنال RFD‌ و ND فعال باشند، صورت می‌پذیرد.

نتایج شبیه سازی این IP Core‌ در سیمولاتور ISIM در شکل زیر نشان داده شده است. به نحوه تغییر وضعیت سیگنال‌های کنترلی ورودی و خروجی در این شکل موج‌ها دقت کنید. شباهت بسیار زیادی به تصویر قبلی دارند.

همانطور که ملاحظه می‌کنید، مقدار ورودی PHASE_IN بر حسب رادیان برابر است با

00011001002=000.11001002=0.7812510 Rad

بنابراین ما انتظار داریم خروجی‌های X_OUT‌ و Y_OUT به صورت زیر باشند:

X_out=cos(0.78125)=0.70915311

Y_out=sin(0.78125)=0.70416751

شبیه سازی مقادیر X_OUT‌ و Y_OUT را به صورت زیر نمایش می‌دهد.

X_out=00.101101102=0.710937510

 Y_out=00.101101002=0.7031250010

اگر این پاسخ‌ها به اندازه کافی برای شما دقیق نیستند فراموش نکنیدکه با افزایش طول بیت و تعداد دفعات تکرار الگوریتم می‌توانید به نتایج دقیق تری دست یابید.

جمع بندی

در ISE تعداد زیادی IP Core کاملاً بهینه و دقیق برای پیاده سازی بسیاری از توابع پایه و پرکاربرد در اختیار شما قرار داده شده است که می‌توانید به فراخور نیازتان از آن‌ها بهره مند شوید. فانکشن‌هایی همچون ضرب کننده‌ها، فیلترهای دیجیتال، تبدیل فوریه گسسته، حافظه ‌ها و موارد فراوان دیگر. استفاده از این IP Core ها به شما امکان رویارویی با پروژه‌های بزرگ و اتمام موفقیت آمیز آن‌ها در زمانی کوتاه تر را می‌دهد. ما در این مقاله به شما نشان دادیم که چگونه می‌توانید از Xilinx IP Core ها برای اضافه کردن توابع سینوس و کسینوس در FPGA به طرحتان استفاده کنید.

منبع: Xilinx ، Allaboutcircuits