نکات و تکنیک‌های طراحی با Vivado HLS (بخش دوم: کتابخانه‌های Arbitrary Precision)

مقدمه

در بخش اول این آموزش که چند هفته پیش منتشر شد، نگاهی موشکافانه به قدرت پنهان ابزار Vivado HLS و ویژگی‌های منحصر به فرد آن در تسریع فرایند پیاده سازی انداختیم و باهم پیاده سازی و بهینه سازی یک معادله صنعتی کاملاً پیچیده را به انجام رساندیم. با توجه به اینکه پیاده سازی ما به صورت ممیز شناور انجام شد، منابع مصرفی به شدت بالا بود، استفاده از متغیرهای float‌ و floating point IP Core های Xilinx بیش از چیزی که در ابتدا پیش بینی می‌کردیم روی منابع مصرفی و ظرفیت خروجی مدار ما تأثیر منفی گذاشت. در بخش دوم این آموزش یک گام دیگر رو به جلو بر می‌داریم و چگونگی کار با نمایش ممیز ثابت اعداد در HLS را مرور می‌کنیم و گزینه‌هایی را که برای این نوع از پیاده سازی در اختیار داریم با جزئیات بررسی می‌کنیم. در این مسیر از کتابخانه‌های Arbitrary Precision در HLS نیز بهره خواهیم برد.

کتابخانه‌های arbitrary precision

وقتی از نمایش ممیز ثابت اعداد برای پیاده سازی استفاده می‌کنیم، در واقع فرم کوآنتیزه شده اعداد ممیز شناور را در محاسبات بکارگرفته‌ایم. طبیعی است که این کار باعث از دست رفتن بخشی از دقت محاسبات می‌شود. در Vivado HLS یک ویژگی بسیار جداب و منحصربه فرد وجود دارد که براساس آن به طراح اجازه داده می‌شود از طول بیت‌های دلخواه به جای طول بیت‌های استاندارد در زبان ++C/C استفاده کند. این کار دست طراح را در انتخاب طول بیت مناسب برای متغیرها باز می‌گذارد و خطای ناشی از کوآنتیزاسیون در صحت محاسبات را کمینه شود. این قابلیت در ادبیات HLS تحت عنوان arbitrary precision شناخته می‌شود. ترجمه تحت لفظی این عبارت انتخاب اختیاری دقت است، ولی مفهوم ساده آن انتخاب اختیاری تعداد بیت‌ها برای یک متغیر است. این دقیقاً مشابه کاری است که در زمان استفاده از کدهای سطح پایین HDL انجام می‌دهیم. ما در ادامه به این موضوع باز می‌گردیم.

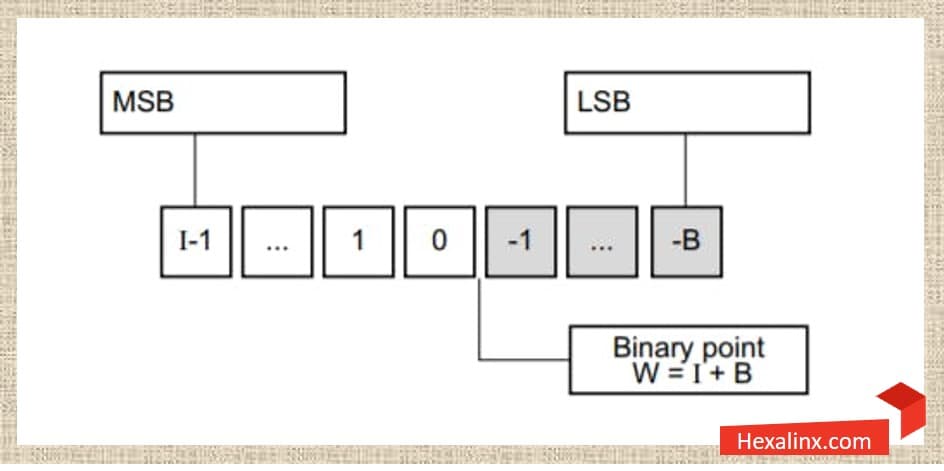
نمایش ممیز ثابت استاندارد

در رابطه با روش استاندارد برای نمایش اعداد ممیز ثابت در آموزش‌های قبلی هگزالینکس توضیحات کاملی ارائه داده‌ایم. شما می‌توانید برای کسب اطلاعات کامل به این مقالات مراجعه کنید. اما صرفاً به عنوان یادآوری اشاره کوتاهی به برخی از نکات کلیدی می‌کنیم.

• اعداد اعشاری ممیز ثابت (بخش سوم: قوانین پایه محاسبات)
• اعداد اعشاری ممیز ثابت (بخش دوم: محاسبات با دقت محدود)
• اعداد اعشاری ممیز ثابت (بخش اول: مفاهیم کلی)
• مبانی محاسبات ریاضی در FPGA (قسمت دوم)
• مبانی محاسبات ریاضی در FPGA (قسمت اول)

روش‌های متعددی برای نشان دادن فرمت‌های ممیز ثابت استفاده می‌شود، که بیشتر وابسته به سلیقه طراح است و یک قانون کلی برای آن وجود ندارد. فرمت مرسوم نمایش بیت‌های صحیح و اعشاری در یک عدد ممیز ثابت به صورت نمایش x,y است که در آن x تعداد بیت‌های صحیح و y تعداد بیت‌های اعشاری را نشان می‌دهد. به عنوان مثال عددی با فرمت 8,8 دارای ۸ بیت صحیح و ۸ بیت اعشار است، در حالی که فرمت 16,0 نمایانگر اختصاص ۱۶ بیت صحیح و صفر بیت اعشار است.

برای نشان دادن علامت دار یا بدون علامت بودن عدد هم ممکن است به ترتیب از دو حرف Q و U استفاده می‌شود. به عنوان مثال عددی با فرمت U8,8 قابلیت نمایش اعداد بین 0 تا 255.9906375 را دارد.

نمایش ممیز ثابت در Vivado HLS

انجام محاسبات ممیز ثابت در HLS و نمایش آن‌ها با استفاده از انواع استاندارد متغیرها در زبان C در قالب بردارهای ۸، ۱۶، ۳۲ و یا ۶۴ بیتی کار چندان هوشمندانه‌ای به نظر نمی‌رسد. چون ما تمایل داریم تمام جزئیات طول بیت‌ها را خودمان مدیریت کنیم. این دقیقاً همان ایده ‌ایست که براساس آن کتابخانه‌های arbitrary precision در Vivado HLS پایه ریزی شده‌اند. با فراخوانی و بکارگیری این کتابخانه‌ها ما قادرخواهیم بود با توجه به زبان برنامه نویسی انتخابی C یا ++C انبوهی از گزینه‌ها را برای سفارشی سازی طول بیت‌ها و همینطور نحوه شرکت آن‌ها در محاسبات کنترل کنیم.

البته بحث در این رابطه بسیار زیاد است و معرفی تمامی قابلیت‌هایی که این کتابخانه در اختیار ما می‌گذارد خارج از حوصله این آموزش است. اما شما می‌توانید از اطلاعاتی که در ادامه به شما می‌دهم به عنوان یک نقطه شروع و ایده اولیه استفاده کنید و خودتان سایر جزئیات را مطالعه کنید.

کتابخانه‌های arbitrary precision برای تمامی زبان‌های قابل پشتیبانی در Vivado HLS یعنی C و ++C و System C قابل استفاده هستند. با این کتابخانه‌ها تعریف متغیرهای ممیز ثابت علامت دار یا بدون علامت با طول بیت ۵۱۲ یا حتی ۱۰۲۴ بیت امکان پذیر است.

انواع قابل استفاده در کتابخانه‌های arbitrary precision با توجه به نوع زبان برنامه نویسی انتخابی در جدول زیر قابل مشاهده هستند. نام کتابخانه نیز در هر زبان با زبان دیگر متفاوت است.

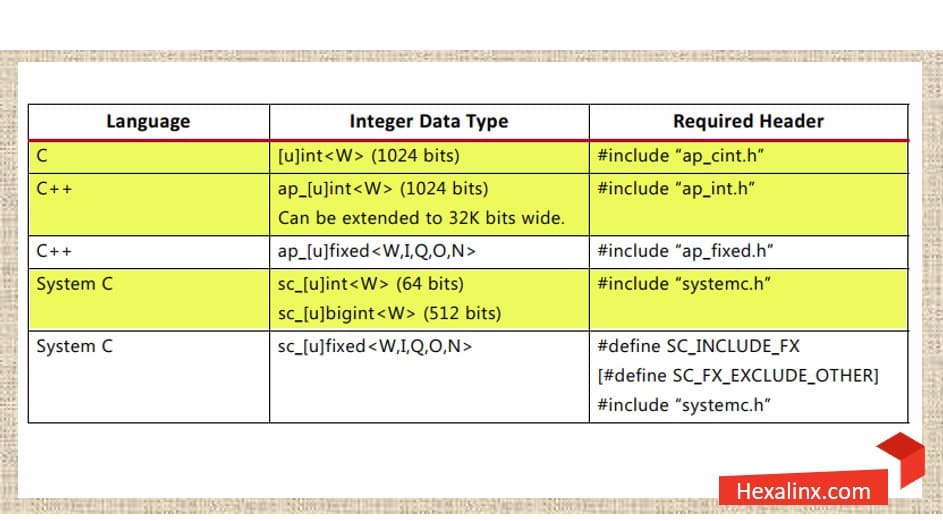
خب به بهترین و مهمترین بخش این آموزش رسیدیم. قصد داریم در ادامه در رابطه با نحوه استفاده از این کتابخانه‌ها در انجام محاسبات ریاضی صحبت کنیم.

انجام محاسبات

ما می‌توانیم از کتابخانه‌های بالا برای تعریف هر نوع متغیری استفاده کنیم و متغیرهای ما همچون قبل می‌توانند برای اجرای عملیات کنترلی و همچنین محاسبات ریاضی بکار گرفته شوند. حتماً با من موافق هستید که در طراحی‌های RTL سطح پایین برای کنترل طول بیت‌ها و نقطه اعشار در محاسبات ممیز ثابت همواره باید دقت و زمان کافی را به خرج دهیم. هر چه قدر مدار ما بزرگتر شود این کار سخت تر می‌شود. صادقانه بگویم بعد از مدتی از این همه انرژی که باید کنترل تعداد بیت‌ها صرف کنید خسته خواهید شد. بعد از هر بار شرکت متغیرها در محاسبات ریاضی باید یک بار همه چیز را کنترل کنیم تا مبادا دقتی را ناخواسته از دست بدهیم یا سرریزی رخ دهد. حالا سوأل انیجاست، ما سنتز سطح بالا و ابزار Vivado HLS را به عنوان روشی برای تسریع پیاده سازی و ساده سازی فرایندهای سرگیجه آور در طراحی HDL معرفی کردیم، اگر قرار باشد بازهم درگیر جزئیات و پیچیدگی‌های محاسبات ممیز ثابت بشویم، دوباره روز از نو روزی از نو !!!

بخشی از ملاحظاتی را که باید هنگام پیاده سازی ممیز ثابت یک الگوریتم در نظر بگیرید برای شما به صورت فهرست وار یادآوری می‌کنم.

• در شروع کار هنگام تبدیل متغیرهای ممیز شناور به ممیز ثابت حتماً به اندازه کافی دقت کنید.
• اثرات رند کردن یا ترانکیشن را متغیرها در نظرات بگیرید.
• برخی از عملگرهای ریاضی همچون جمع نیاز دارند نقاط اعشار عملوندها قبل از شرکت در عملیات باهم تراز شوند.
• انتخاب سایز و طول بیت مناسب برای ذخیره نتایج محاسبات را نیز حتماً باید مدنظر قرار بگیرد.

مواردی که اشاره شد جز جدایی ناپذیر هر طراحی ممیز ثابت است. چه سطح بالا کد بنویسیم و چه سطح پایین، فرقی نمی‌کند! چون همواره برای به دست آوردن هر چیز باید هزینه آن را بپردازیم و هزینه بهینه سازی در هر دو حالت افزایش پیچیدگی و کاهش سرعت است. اما خیلی ناامید نشوید. خبر خوب این است که برای انجام عملیات و محاسبات ریاضی در صورت استفاده از زبان‌های ++C و System C کتابخانه‌های arbitrary precision یک جایگزین مناسب‌ تر در اختیار طراح قرار می‌دهند و آن چیزی نیست جز کتابخانه اختصاصی arbitrary precision Fixed Point .

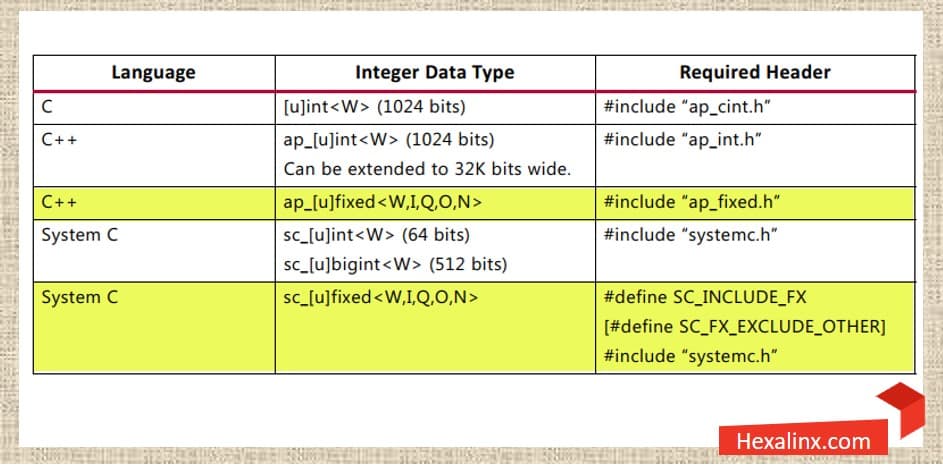
شما به عنوان یک طراح و پیاده ساز می‌توانید با استفاده از این کتابخانه‌ها از یکسان بودن نتایج شبیه سازی و نتایج پیاده‌سازی کاملاً مطمئن باشید. تنها کاری که لازم است انجام دهید، رعایت قوانین اختصاصی HLS در استفاده از انواع ممیز ثابت درون کتابخانه arbitrary precision Fixed Point است. انواع ممیز ثابت دارای مجموعه‌ای از پارامترها هستند که شما قادر به کنترل آن‌ها هستید، لیست این پارامترها به شرح زیر است:

• تعداد کل بیت‌های متغیر (W)
• تعداد بیت‌های صحیح  متغیر (I)
• مد کوآنتیزاسیون (Q) : از بین گزینه‌های مجاز باید یکی را انتخاب کنید. مثلاً می‌توانید رندکردن یا ترانکیشن را انتخاب کنید.
• نوع سرریز (O) : واکنش متغیر در صورت بروز سرریز با این پارامتر تعیین می‌شود. انتخاب‌های شما در اینجا گزینه‌هایی همچون اشباع (saturation) یا پیچیده شدن (wrap) است.
• بیت اشباع (N) : در صورت انتخاب مد سرریز wrap کاربرد دارد.

با استفاده از کتابخانه arbitrary precision Fixed Point به جای arbitrary precision در زمان پیاده سازی محاسبات ریاضی، کار با اعداد ممیز ثابت به وضوح ساده تر می‌شود، چون ما دو مزیت مهم بدست می‌‌آوریم:

• نیازی به کنترل نقطه اعشار در زمان انجام محاسبات نداریم.
• کار نمایش اعداد در فرمت ممیز ثابت به مراتب ساده تر است.

یعنی مشابه جعبه ابزار fixed point در Matlab بخشی از ملاحظات مورد نیاز به صورت اتوماتیک توسط ابزار Vivado HLS مدیریت می‌شود.

برای درک کامل موضوع اجازه بدهید یک مثال ساده را با هم مرور کنیم. در این مثال یک فیلتر میانگین گیر متحرک را پیاده سازی می‌کنیم.

مثالی از فیلتر میانگین گیر متحرک

یک فیلتر میانگین گیر متحرک آرایه‌ای از ورودی‌ها را با یکدیگر جمع می‌کند و با تقسیم بر تعداد ورودی‌ها، میانگین آن‌ها را محاسبه می‌کند. ما قبلاً این فیلتر را به شما معرفی کرده‌ایم و شما می‌توانید پیاده سازی ممیز ثابت آن را به زبان VHDL در اینجا مطالعه کنید. از این فیلتر معمولاً برای کاهش نویزهای فرکانس بالا و یا نویزهای تصادفی استفاده می‌شود. عملیات فیلتر کردن به ازای هر نمونه جدید در ورودی یکبار اجرا می‌شود و با محاسبه میانگین روی یک بافر n تایی فیلتر، خروجی تولید می‌شود. طول بافر مورد استفاده در فیلتر با توجه به کاربرد مدنظر طراح تعیین می‌شود، هر چقدر این بافر بزرگتر باشد پاسخ خروجی نرم‌تر می‌شود ولی در عین حال فیلتر کندتر نیز می‌شود. فرض کنید در اینجا قصد داریم یک فیلتر میانگین گیر با ۱۰ ورودی که هر کدام از آن‌ها دارای ۸ بیت صحیح و ۲ بیت اعشاری هستند، پیاده سازی کنیم. یعنی فیلتری با ورودی‌های ۱۰ بیتی.

در ادامه می‌توانید کد ساده‌ای را که برای این فیلتر با استفاده از کتابخانه‌ arbitrary precision Fixed Point نوشته شده است، مشاهده کنید. در این کد:

• ورودی فیلتر آرگومان ip است که از نوع ap_ufixed انتخاب شده است.
• خروجی فیلتر آرگومان op است که از بازهم از نوع ap_ufixed انتخاب شده است.
• از اینترفیس ap_fifo و دایرکتیو interface برای پورت ورودی استفاده شده است.
• از دایرکتیو pipeline هم برای پایپلاین کردن جمع کننده انباره استفاده شده است.
• و در نهایت از ثابت 0.1 به عنوان ضریبی برای خروجی جهت مدل کردن عملیات تقسیم بر ۱۰ استفاده شده است.

نکته بسیار مهم در این کد سایز متغیر میانی sum و بردار خروجی op است که به ترتیب ۱۴ و ۲۴ بیت در نظر گرفته شده‌اند. این کار برای کنترل رشد بیت جمع کننده انباره در جمع‌های متوالی انجام شده است. آیا می‌توانید رشد بیت مورد نیاز را حساب کنید؟ لطفاً در کامنت‌های ذیل این مطلب نحوه محاسبه رشد بیت برای این دو متغیر را برای ما بنویسید.

// copyright 2020 Hexalinx.com

#include <ap_fixed.h>

void moving_average_filter(ap_ufixed<10,8> ip[10], ap_ufixed<24,12> op) {
#pragma HLS INTERFACE ap_fifo port=ip
	int i;
	ap_ufixed<10,0> divider = 0.1;
	ap_ufixed<14,12> sum = 0;
	filter_loop:for (i = 0; i < 10; i++) {
#pragma HLS PIPELINE
		sum = sum + ip[i];
	}
	op = sum * divider;

}

بعد از اجرای عملیات سنتز، مقدار پارامتر initiation interval برابر با یک می‌شود که کاملاً مطلوب است.

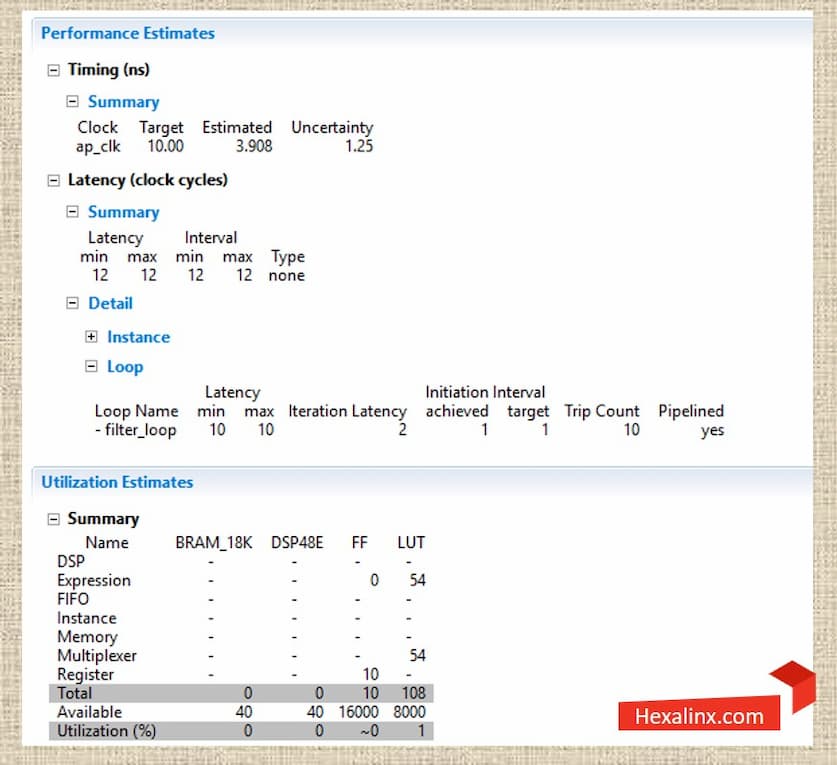
مشابه کد بالا، از همین الگو می‌توانیم برای بازنویسی چند جمله‌ای تقریب زده شده از رابطه Van Dusen که در بخش اول این آموزش معرفی کردیم نیز استفاده کنیم و نتایج آن را با نتایج قبلی مقایسه کنیم. همچون قبل دوباره می‌توانیم از اینترفیس FIFO‌ و آرایه‌هایی با طول دلخواه برای آرگومان‌ها ورودی خروجی فانکشن (یا همون پورت‌های ماژول RTL استفاده کنیم). همینطور با استفاده از دایرکتیو‌های پایپلاین، پارتیشن بندی آرایه‌ها و باز کردن حلقه‌ محاسباتی برنامه، می‌توانیم انواع بهینه سازی‌ها را روی کدهای HLS اعمال کنیم.

بعد از اعمال تمامی پراگماهای مورد نیاز خواهید دید که اینبار با استفاده از متغیرهای ممیز ثابت و کتابخانه‌های arbitrary precision نتایج بسیار قابل قبول تری به دست می‌آوریم. تا جایی که پارامتر II=1 نیز در گزارش سنتز نمایان می‌شود. و این یعنی به حداکثر ظرفیت خروجی قابل حصول دست پیدا کردیم.

جمع بندی

امیدوارم نکات و تکنیک‌هایی که در این دو بخش ارائه شد، به شما در درک بهتر قابلیت‌های ابزار Vivado HLS و نحوه استفاده از آن‌ها کمک کند. با رعایت این نکات ساده دستیابی به بسیاری از نیازهای شما و همینطور غلبه بر چالش‌های طراحی برای شما امکان پذیر می‌شود. توجه داشته باشید که کتابخانه‌های arbitrary precision فقط مخصوص Vivado HLS هستند و شما نمی توانید در کیت توسعه Xilinx یا همان (SDK) از آن‌ها استفاده کنید.

ممکن است در زمان دیباگ کدهای نوشته شده مشاهده مقادیر متغیرهای جدید ممیز ثابت برای شما امکان پذیر نباشد. برای این کار متدهای استانداردی در کتابخانه‌های arbitrary precision تعریف شده است که شما می‌توانید با مراجعه به سند UG902 اطلاعات تکمیلی برای این کار را به دست بیاورید.

منبع: با اقتباس از hackster.io نوشته  Adam Taylor